Zero moment point is a concept related with dynamics and control of legged locomotion, e.g., for humanoid robots. It specifies the point with respect to which dynamic reaction force at the contact of the foot with the ground does not produce any moment in the horizontal direction, i.e. the point where the total of horizontal inertia and gravity forces equals 0 (zero). The concept assumes the contact area is planar and has sufficiently high friction to keep the feet from sliding.
Introduction
This concept was introduced in January 1968 by Miomir Vukobratović at The Third All-Union Congress of Theoretical and Applied Mechanics in Moscow. In the following works and papers that were produced between 1970 and 1972 it would then be called zero moment point and would be spread around the world.
The zero moment point is a very important concept in the motion planning for biped robots. Since they have only two points of contact with the floor and they are supposed to walk, “run” or “jump” (in the motion context), their motion has to be planned concerning the dynamical stability of their whole body. This is not an easy task, especially because the upper body of the robot (torso) has larger mass and inertia than the legs which are supposed to support and move the robot. This can be compared to the problem of balancing an inverted pendulum.
The trajectory of a walking robot is planned using the angular momentum equation to ensure that the generated joint trajectories guarantee the dynamical postural stability of the robot, which usually is quantified by the distance of the zero moment point in the boundaries of a predefined stability region. The position of the zero moment point is affected by the referred mass and inertia of the robot’s torso, since its motion generally requires large ankle torques to maintain a satisfactory dynamical postural stability.
One approach to solve this problem consists in using small trunk motions to stabilize the posture of the robot. However, some new planning methods are being developed to define the trajectories of the legs’ links in such a way that the torso of the robot is naturally steered in order to reduce the ankle torque needed to compensate its motion. If the trajectory planning for the leg links is well succeeded, then the zero moment point won’t move out of the predefined stability region and the motion of the robot will become smoother, mimicking a natural trajectory.
ZMP computation
The resultant force of the inertia and gravity forces acting on a biped robot is expressed by the formula:
where is the total mass of the robot, is the acceleration of the gravity, is the center of mass and is the acceleration of the center of mass.
The moment in any point can be defined as:
where is the rate of angular momentum at the center of mass.
The Newton–Euler equations of the global motion of the biped robot can be written as:
where is the resultant of the contact forces at X and is the moment related with contact forces about any point X.
The Newton–Euler equations can be rewritten as:
so it’s easier to see that we have:
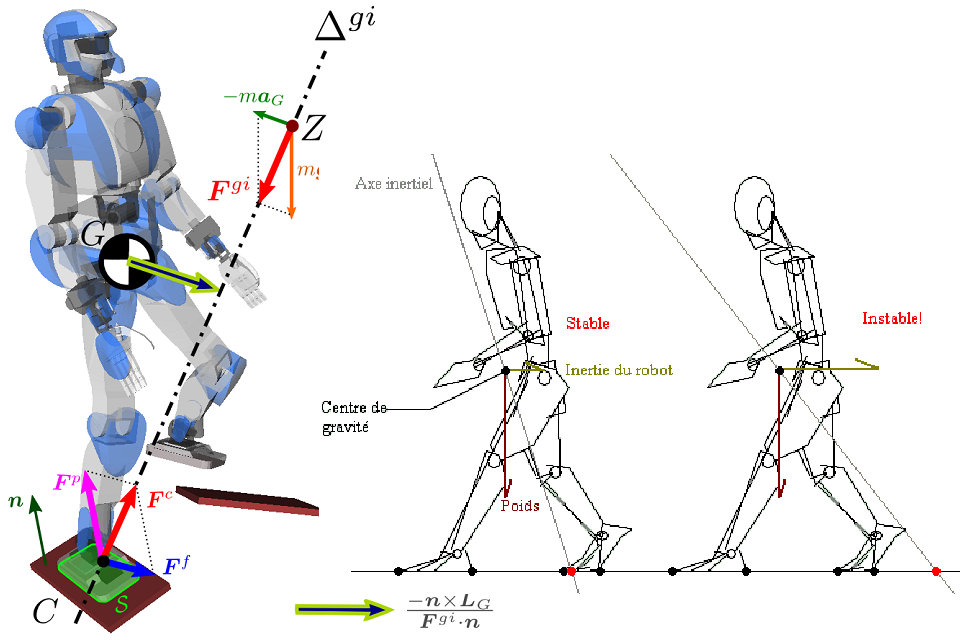
These equations show that the biped robot is dynamically balanced if the contact forces and the inertia and gravity forces are strictly opposite.
If an axis is defined, where the moment is parallel to the normal vector from the surface about every point of the axis, then the Zero Moment Point (ZMP) necessarily belongs to this axis, since it is by definition directed along the vector . The ZMP will then be the intersection between the axis and the ground surface such that:
with
where represents the ZMP.
Because of the opposition between the gravity and inertia forces and the contact forces mentioned before, the {\displaystyle Z} point (ZMP) can be defined by:
where is a point on the contact plane, e.g. the normal projection of the center of mass.
History of the concept
The notion of ZMP was first introduced by Miomir Vukobratović at the Third Congress of the Union for Theoretical and Applied Mechanics held in Moscow in January 1968. The term “zero moment point” appeared in published works. during the following years.
Interest in the ZMP took off in the 1990s, when roboticists successfully applied it to control laws for bipedal walking. The fundamental model that allowed these developments is that of the inverted pendulum: the upper body having a mass greater than the legs, walking consists in first approximation to the movement of an inverted pendulum, that is to say a connected mass to a mobile base by a rod of zero mass (the model “CART”). The mass in question represents the center of gravity of the robot, the rod its support leg, and the mobile base point is none other than the ZMP. This model was successfully applied to the HRP-2 1 and HRP-4C robots .] where the center of gravity remains at constant height.
Link with the pressure center
The center of pressure is a dynamic point characteristic of a contact. Unlike the ZMP, which is defined according to all accelerations of the robot, the COP is a local quantity defined from the forces exerted on the surface of a contact. However, when there is only one contact, or the robot is walking on horizontal ground, the COP and the ZMP coincide.
The figure on the right represents the center of gravity , the pressure center of the foot-right contact as well as an ZMP . Dots are always aligned on the inertial axis . The latter does not necessarily pass through the center of gravity, unless the robot keeps its angular momentum (), which is a common working hypothesis in locomotion .
Special case of flat ground
As long as the contact with the surface does not break, the center of pressure necessarily resides inside the contact surface between the robot and the environment. When the two feet of the robot are in contact with the same surface (the ground), this surface of levitation is the convex hull of all the points of support, that is to say the set of points situated “between the two feet”. This surface makes it possible to define the pressures and friction, and therefore an associated pressure center (see Pressure Center for more details). COP and ZMP coinciding, we get the criterion:
Non-tilt criterion: During tilt-free operation, the ZMP is located within the lift surface, defined as the convex hull of the fulcrums.
This criterion is most frequently used for the walking of humanoid robots on flat ground.
Applications
Zero moment point has been proposed as a metric that can be used to assess stability against tipping over of robots like the iRobot PackBot when navigating ramps and obstacles.
Source from Wikipedia

 is the total mass of the robot,
is the total mass of the robot,  is the acceleration of the gravity,
is the acceleration of the gravity,  is the center of mass and
is the center of mass and  is the acceleration of the center of mass.
is the acceleration of the center of mass. can be defined as:
can be defined as:
 is the rate of angular momentum at the center of mass.
is the rate of angular momentum at the center of mass.

 is the resultant of the contact forces at X and
is the resultant of the contact forces at X and  is the moment related with contact forces about any point X.
is the moment related with contact forces about any point X.



 is defined, where the moment is parallel to the normal vector
is defined, where the moment is parallel to the normal vector  from the surface about every point of the axis, then the Zero Moment Point (ZMP) necessarily belongs to this axis, since it is by definition directed along the vector
from the surface about every point of the axis, then the Zero Moment Point (ZMP) necessarily belongs to this axis, since it is by definition directed along the vector 

 represents the ZMP.
represents the ZMP.
 is a point on the contact plane, e.g. the normal projection of the center of mass.
is a point on the contact plane, e.g. the normal projection of the center of mass.

