Le point zéro moment est un concept lié à la dynamique et au contrôle de la locomotion à jambes, par exemple pour les robots humanoïdes. Il spécifie le point par rapport auquel la force de réaction dynamique au contact du pied avec le sol ne produit aucun moment dans la direction horizontale, c’est-à-dire le point où le total des forces d’inertie et de gravité horizontales est égal à 0 (zéro). Le concept suppose que la zone de contact est plane et que le frottement est suffisamment important pour empêcher les pieds de glisser.

introduction
Ce concept a été introduit en janvier 1968 par Miomir Vukobratović lors du troisième congrès national de la mécanique théorique et appliquée à Moscou. Dans les œuvres et papiers suivants, produits entre 1970 et 1972, il s’appellerait alors Point instantané et serait diffusé dans le monde entier.

Le point zéro moment est un concept très important dans la planification de mouvement pour les robots bipèdes. Puisqu’ils n’ont que deux points de contact avec le sol et qu’ils sont supposés marcher, «courir» ou «sauter» (dans le contexte du mouvement), leur mouvement doit être planifié en ce qui concerne la stabilité dynamique de tout leur corps. Ce n’est pas une tâche facile, en particulier parce que la partie supérieure du corps du robot (torse) a une masse et une inertie supérieures à celles des jambes qui sont supposées supporter et déplacer le robot. Ceci peut être comparé au problème de l’équilibrage d’un pendule inversé.

La trajectoire d’un robot marcheur est planifiée à l’aide de l’équation du moment cinétique pour garantir que les trajectoires articulaires générées garantissent la stabilité posturale dynamique du robot, qui est généralement quantifiée par la distance du point du moment zéro dans les limites d’une région de stabilité prédéfinie. La position du point zéro du moment dépend de la masse et de l’inertie du torse du robot, car son mouvement nécessite généralement des couples importants à la cheville pour maintenir une stabilité posturale dynamique satisfaisante.

Une approche pour résoudre ce problème consiste à utiliser de petits mouvements du tronc pour stabiliser la posture du robot. Cependant, de nouvelles méthodes de planification sont en cours de développement pour définir les trajectoires des liens de jambes de telle sorte que le torse du robot soit naturellement dirigé afin de réduire le couple de cheville nécessaire pour compenser son mouvement. Si la planification de la trajectoire pour les liaisons de jambe est bien effectuée, le point du moment zéro ne sortira pas de la région de stabilité prédéfinie et le mouvement du robot deviendra plus fluide, imitant une trajectoire naturelle.

Calcul ZMP
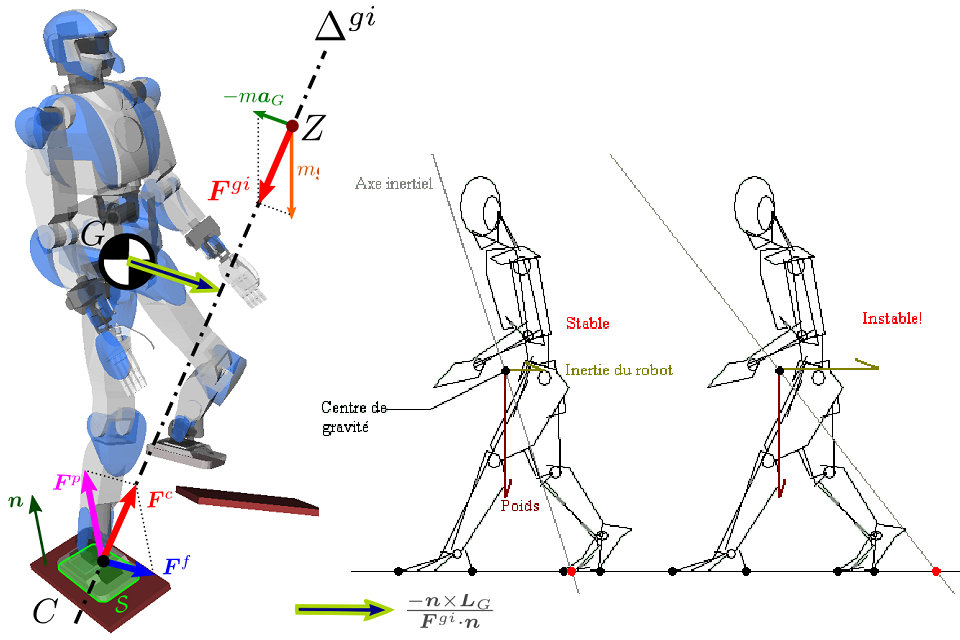
La force résultante des forces d’inertie et de gravité agissant sur un robot bipède s’exprime par la formule:

où  est la masse totale du robot,  est l’accélération de la gravité,  est le centre de masse et  est l’accélération du centre de masse.

Le moment en tout point  peut être défini comme:

où  est la vitesse du moment angulaire au centre de la masse.
Les équations de Newton – Euler du mouvement global du robot bipède peuvent s’écrire comme suit:

où  est la résultante des forces de contact en X et  est le moment lié aux forces de contact sur un point quelconque X.
Les équations de Newton – Euler peuvent être réécrites comme suit:

il est donc plus facile de voir que nous avons:

Ces équations montrent que le robot bipède est équilibré dynamiquement si les forces de contact et les forces d’inertie et de gravité sont strictement opposées.

Si un axe  est défini, où le moment est parallèle au vecteur normal  de la surface autour de chaque point de l’axe, le point du moment zéro (ZMP) appartient nécessairement à cet axe, puisqu’il est par définition dirigé le long du vecteur  . Le ZMP sera alors l’intersection entre l’axe  et la surface du sol telle que:

avec

où  représente le ZMP.

En raison de l’opposition entre les forces de gravité et d’inertie et les forces de contact mentionnées précédemment, le {\ displaystyle Z}  point (ZMP) peut être défini par:

où  est un point sur le plan de contact, par exemple la projection normale du centre de masse.

Histoire du concept
La notion de ZMP a été introduite pour la première fois par Miomir Vukobratović lors du troisième congrès de l’Union de mécanique théorique et appliquée, tenu à Moscou en janvier 1968. L’expression « point d’instant zéro » est apparue dans des ouvrages publiés. au cours des années suivantes.

L’intérêt pour le ZMP a pris son envol dans les années 1990, lorsque les roboticiens l’ont appliqué avec succès pour contrôler les lois régissant la marche bipède. Le modèle fondamental qui a permis ces développements est celui du pendule inversé: la partie supérieure du corps ayant une masse plus grande que les jambes, la marche consiste en une première approximation du mouvement d’un pendule inversé, c’est-à-dire une masse reliée à une base mobile par une canne de masse nulle (le modèle « CART »). La masse en question représente le centre de gravité du robot, la tige sa jambe de force et le point de base mobile n’est autre que le ZMP. Ce modèle a été appliqué avec succès aux robots HRP-2 1 et HRP-4C.] Où le centre de gravité reste à une hauteur constante.

Lien avec le centre de pression
Le centre de pression est un point dynamique caractéristique d’un contact. Contrairement au ZMP, qui est défini en fonction de toutes les accélérations du robot, le COP est une quantité locale définie à partir des forces exercées à la surface d’un contact. Cependant, lorsqu’il n’y a qu’un seul contact ou que le robot marche sur un sol horizontal, le COP et le ZMP coïncident.

La figure à droite représente le centre de gravité  , le centre de pression du contact pied-droit  ainsi qu’un ZMP  . Points  sont toujours alignés sur l’axe inertiel  . Ce dernier ne passe pas nécessairement par le centre de gravité, sauf si le robot conserve son moment angulaire (  ), qui est une hypothèse de travail commune en locomotion.

Cas particulier de terrain plat
Tant que le contact avec la surface ne se rompt pas, le centre de pression réside nécessairement dans la surface de contact entre le robot et l’environnement. Lorsque les deux pieds du robot sont en contact avec la même surface (le sol), cette surface de lévitation  est la coque convexe de tous les points d’appui, c’est-à-dire de l’ensemble des points situés « entre les deux pieds ». Cette surface permet de définir les pressions et les frottements, et donc un centre de pression associé (voir Centre de pression pour plus de détails). COP et ZMP coïncidant, nous obtenons le critère:

Critère de non-inclinaison: En fonctionnement sans inclinaison, le ZMP est situé dans la surface de soulèvement, définie comme la coque convexe des points d’appui.

Ce critère est le plus souvent utilisé pour la marche de robots humanoïdes sur un terrain plat.

Applications
Le point zéro moment a été proposé en tant que métrique permettant d’évaluer la stabilité contre le renversement de robots tels que le iRobot PackBot lors de la navigation sur des rampes et des obstacles.