El punto de momento cero es un concepto relacionado con la dinámica y el control de la locomoción en las piernas, por ejemplo, para robots humanoides. Especifica el punto con respecto al cual la fuerza de reacción dinámica en el contacto del pie con el suelo no produce ningún momento en la dirección horizontal, es decir, el punto donde el total de inercia horizontal y fuerzas de gravedad es igual a 0 (cero). El concepto asume que el área de contacto es plana y tiene una fricción suficientemente alta para evitar que los pies se deslicen.

Introducción
Este concepto fue introducido en enero de 1968 por Miomir Vukobratović en el Tercer Congreso de la Unión de Mecánica Teórica y Aplicada en Moscú. En las siguientes obras y documentos que se produjeron entre 1970 y 1972, se llamaría punto cero y se difundirían por todo el mundo.

El punto de momento cero es un concepto muy importante en la planificación del movimiento para robots bípedos. Dado que solo tienen dos puntos de contacto con el piso y se supone que deben caminar, «correr» o «saltar» (en el contexto del movimiento), su movimiento debe planificarse en relación con la estabilidad dinámica de todo su cuerpo. Esta no es una tarea fácil, especialmente porque la parte superior del cuerpo del robot (torso) tiene una masa e inercia más grandes que las patas que se supone que sostienen y mueven al robot. Esto puede compararse con el problema de equilibrar un péndulo invertido.

La trayectoria de un robot ambulante se planifica utilizando la ecuación de momento angular para garantizar que las trayectorias conjuntas generadas garanticen la estabilidad postural dinámica del robot, que generalmente se cuantifica por la distancia del punto de momento cero en los límites de una región de estabilidad predefinida. La posición del punto de momento cero se ve afectada por la masa referida y la inercia del torso del robot, ya que su movimiento generalmente requiere pares de tobillo grandes para mantener una estabilidad postural dinámica satisfactoria.

Un enfoque para resolver este problema consiste en utilizar pequeños movimientos del tronco para estabilizar la postura del robot. Sin embargo, se están desarrollando algunos nuevos métodos de planificación para definir las trayectorias de los enlaces de las piernas de tal manera que el torso del robot sea dirigido naturalmente para reducir el torque del tobillo necesario para compensar su movimiento. Si la planificación de la trayectoria de los enlaces de las piernas es exitosa, entonces el punto de momento cero no se moverá fuera de la región de estabilidad predefinida y el movimiento del robot se volverá más suave, imitando una trayectoria natural.

Computación ZMP
La fuerza resultante de la inercia y las fuerzas de gravedad que actúan en un robot bípedo se expresan mediante la fórmula:

dónde  es la masa total del robot,  Es la aceleración de la gravedad.  es el centro de masa y  Es la aceleración del centro de masa.

El momento en cualquier punto.  Puede ser definido como:

dónde  Es la tasa de momento angular en el centro de masa.
Las ecuaciones de Newton-Euler del movimiento global del robot bípedo se pueden escribir como:

dónde  es la resultante de las fuerzas de contacto en X y  Es el momento relacionado con las fuerzas de contacto sobre cualquier punto X.
Las ecuaciones de Newton-Euler pueden reescribirse como:

así que es más fácil ver que tenemos:

Estas ecuaciones muestran que el robot bípedo está equilibrado dinámicamente si las fuerzas de contacto y la fuerza de inercia y gravedad son estrictamente opuestas.

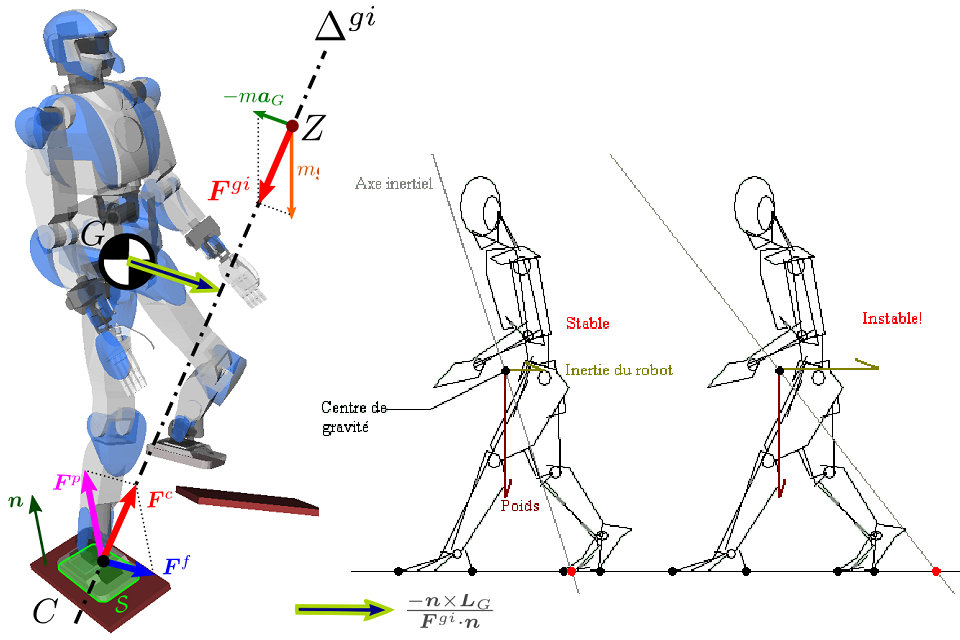
Si un eje  Se define, donde el momento es paralelo al vector normal.  desde la superficie sobre cada punto del eje, entonces el punto de momento cero (ZMP) pertenece necesariamente a este eje, ya que, por definición, se dirige a lo largo del vector  . La ZMP será entonces la intersección entre el eje.  y la superficie del suelo tal que:

con

dónde  representa la ZMP.

Debido a la oposición entre las fuerzas de gravedad e inercia y las fuerzas de contacto mencionadas anteriormente, el {\ displaystyle Z}  punto (ZMP) se puede definir por:

dónde  Es un punto en el plano de contacto, por ejemplo, la proyección normal del centro de masa.

Historia del concepto
La noción de ZMP fue presentada por primera vez por Miomir Vukobratović en el Tercer Congreso de la Unión para la Mecánica Teórica y Aplicada celebrado en Moscú en enero de 1968. El término «punto de momento cero» apareció en trabajos publicados. durante los siguientes años.

El interés en la ZMP despegó en la década de 1990, cuando los roboticists lo aplicaron con éxito a las leyes de control para caminar bipedal. El modelo fundamental que permitió estos desarrollos es el del péndulo invertido: la parte superior del cuerpo tiene una masa mayor que las piernas, el caminar consiste en una primera aproximación al movimiento de un péndulo invertido, es decir, una masa conectada a una base móvil por Una vara de masa cero (el modelo «CART»). La masa en cuestión representa el centro de gravedad del robot, la barra de su pata de apoyo y el punto base móvil no es otro que el ZMP. Este modelo se aplicó con éxito a los robots HRP-2 1 y HRP-4C] donde el centro de gravedad permanece a una altura constante.

Enlace con el centro de presión.
El centro de presión es un punto dinámico característico de un contacto. A diferencia de la ZMP, que se define de acuerdo con todas las aceleraciones del robot, la COP es una cantidad local definida a partir de las fuerzas ejercidas sobre la superficie de un contacto. Sin embargo, cuando solo hay un contacto, o el robot está caminando sobre un terreno horizontal, el COP y el ZMP coinciden.

La figura de la derecha representa el centro de gravedad.  , el centro de presión del contacto pie-derecho.  así como un ZMP  . Puntos  Siempre están alineados en el eje inercial.  . Este último no pasa necesariamente por el centro de gravedad, a menos que el robot mantenga su momento angular (  ), que es una hipótesis de trabajo común en la locomoción.

Caso especial de suelo plano.
Mientras el contacto con la superficie no se rompa, el centro de presión necesariamente reside dentro de la superficie de contacto entre el robot y el entorno. Cuando los dos pies del robot están en contacto con la misma superficie (el suelo), esta superficie de levitación  Es el casco convexo de todos los puntos de apoyo, es decir, el conjunto de puntos situados «entre los dos pies».Esta superficie hace posible definir las presiones y la fricción, y por lo tanto un centro de presión asociado (ver Centro de presión para más detalles). Coincidiendo COP y ZMP, obtenemos el criterio:

Criterio de no inclinación: durante la operación sin inclinación, la ZMP se encuentra dentro de la superficie de elevación, definida como el casco convexo de los fulcros.

Este criterio se utiliza con mayor frecuencia para el desplazamiento de robots humanoides en terrenos planos.

Aplicaciones
El punto de momento cero se ha propuesto como una métrica que se puede usar para evaluar la estabilidad contra el volcamiento de robots como el iRobot PackBot cuando se navega por rampas y obstáculos.