Der Null-Moment-Punkt ist ein Konzept, das mit der Dynamik und Kontrolle der Beinbewegung in Verbindung steht, z. B. für humanoide Roboter. Sie gibt den Punkt an, an dem die dynamische Reaktionskraft beim Kontakt des Fußes mit dem Boden in horizontaler Richtung kein Moment erzeugt, dh der Punkt, an dem die Summe der horizontalen Trägheits- und Schwerkraftkräfte gleich 0 (Null) ist. Das Konzept geht davon aus, dass die Kontaktfläche eben ist und eine ausreichend hohe Reibung aufweist, um ein Gleiten der Füße zu verhindern.

Einführung
Dieses Konzept wurde im Januar 1968 von Miomir Vukobratović auf dem Dritten Allunionskongress für Theoretische und Angewandte Mechanik in Moskau vorgestellt. In den folgenden Arbeiten und Veröffentlichungen, die zwischen 1970 und 1972 produziert wurden, wird sie als Nullmomentpunkt bezeichnet und auf der ganzen Welt verbreitet.

Der Nullmomentpunkt ist ein sehr wichtiges Konzept in der Bewegungsplanung für Biped-Roboter.Da sie nur zwei Berührungspunkte mit dem Boden haben und gehen sollen („laufen“ oder „springen“ (im Bewegungszusammenhang)), muss ihre Bewegung hinsichtlich der dynamischen Stabilität ihres gesamten Körpers geplant werden. Dies ist keine leichte Aufgabe, insbesondere weil der Oberkörper des Roboters (Rumpf) eine größere Masse und Trägheit aufweist als die Beine, die den Roboter stützen und bewegen sollen. Dies kann mit dem Problem des Ausgleichs eines umgekehrten Pendels verglichen werden.

Die Flugbahn eines Laufroboters wird mithilfe der Drehimpulsgleichung geplant, um sicherzustellen, dass die erzeugten Gelenkbahnen die dynamische Haltungsstabilität des Roboters gewährleisten, die üblicherweise durch den Abstand des Nullmomentpunkts in den Grenzen eines vordefinierten Stabilitätsbereichs quantifiziert wird. Die Position des Nullmomentpunkts wird durch die Masse und Trägheit des Roboters beeinflusst, da seine Bewegung im Allgemeinen große Knöchelmomente erfordert, um eine zufriedenstellende dynamische Haltungsstabilität aufrechtzuerhalten.

Ein Ansatz zur Lösung dieses Problems besteht darin, kleine Rumpfbewegungen zu verwenden, um die Haltung des Roboters zu stabilisieren. Es werden jedoch einige neue Planungsmethoden entwickelt, um die Flugbahnen der Glieder der Beine so zu definieren, dass der Rumpf des Roboters auf natürliche Weise gesteuert wird, um das Drehmoment des Sprunggelenks zu reduzieren, das zum Ausgleichen seiner Bewegung erforderlich ist. Wenn die Flugbahnplanung für die Beinglieder gut gelingt, wird der Nullmomentpunkt nicht aus dem vordefinierten Stabilitätsbereich entfernt, und die Bewegung des Roboters wird ruhiger und ahmt eine natürliche Flugbahn nach.

ZMP-Berechnung
Die resultierende Kraft der auf einen zweibeinigen Roboter wirkenden Trägheits- und Schwerkraftkräfte wird durch die Formel ausgedrückt:

woher  ist die Gesamtmasse des Roboters,  ist die Beschleunigung der Schwerkraft, ist der Schwerpunkt und  ist die Beschleunigung des Massenschwerpunkts.

Der Moment in jedem Punkt  kann definiert werden als:

woher  ist die Geschwindigkeit des Drehimpulses im Massenmittelpunkt.
Die Newton-Euler-Gleichungen der globalen Bewegung des Biped-Roboters können wie folgt geschrieben werden:

woher  ist das Ergebnis der Kontaktkräfte bei X und  ist der Moment, der mit den Kontaktkräften um jeden Punkt X zusammenhängt.
Die Newton-Euler-Gleichungen können wie folgt umgeschrieben werden:

So ist es einfacher zu sehen, dass wir:

Diese Gleichungen zeigen, dass der Biped-Roboter dynamisch ausbalanciert ist, wenn die Kontaktkräfte und die Trägheits- und Schwerkraftkräfte genau entgegengesetzt sind.

Wenn eine Achse  definiert ist, wo der Moment parallel zum Normalenvektor ist  Von der Oberfläche ausgehend von jedem Punkt der Achse gehört der Null-Moment-Punkt (ZMP) notwendigerweise zu dieser Achse, da er per Definition entlang des Vektors gerichtet ist  . Der ZMP ist dann der Schnittpunkt zwischen der Achse  und die Bodenoberfläche so, dass

mit

woher  repräsentiert das ZMP.

Wegen des Gegensatzes zwischen den Schwerkraft- und Trägheitskräften und den zuvor genannten Kontaktkräften ist der {\ displaystyle Z}  Punkt (ZMP) kann definiert werden durch:

woher  ist ein Punkt auf der Kontaktebene, z. B. die normale Projektion des Massenschwerpunkts.

Geschichte des Konzepts
Der Begriff ZMP wurde erstmals von Miomir Vukobratović auf dem Dritten Kongress der Union für Theoretische und Angewandte Mechanik im Januar 1968 in Moskau vorgestellt. Der Begriff „Zero Moment Point“ erschien in veröffentlichten Arbeiten. in den folgenden Jahren.

Das Interesse an der ZMP nahm in den 1990er-Jahren zu, als Robotiker es erfolgreich zur Kontrolle von Gesetzen für bipedales Gehen anwendeten. Das grundlegende Modell, das diese Entwicklungen zuließ, ist das des umgekehrten Pendels: Der Oberkörper, der eine Masse hat, die größer ist als die Beine, besteht in erster Annäherung an die Bewegung eines umgekehrten Pendels, das heißt einer mit einer beweglichen Basis verbundenen Masse eine Stange mit Nullmasse (das Modell „CART“).Die fragliche Masse stellt den Schwerpunkt des Roboters dar, die Stange ihr Stützbein und der mobile Basispunkt ist kein anderer als der ZMP. Dieses Modell wurde erfolgreich auf die HRP-2 1- und HRP-4C-Roboter angewendet.], Bei denen der Schwerpunkt konstant bleibt.

Verbindung mit dem Druckzentrum
Der Druckmittelpunkt ist ein dynamischer Punkt, der für einen Kontakt charakteristisch ist. Im Gegensatz zum ZMP, der gemäß allen Beschleunigungen des Roboters definiert ist, ist der COP eine lokale Größe, die aus den auf die Oberfläche eines Kontakts ausgeübten Kräften definiert wird.Wenn es jedoch nur einen Kontakt gibt oder der Roboter auf horizontalem Boden läuft, stimmen COP und ZMP überein.

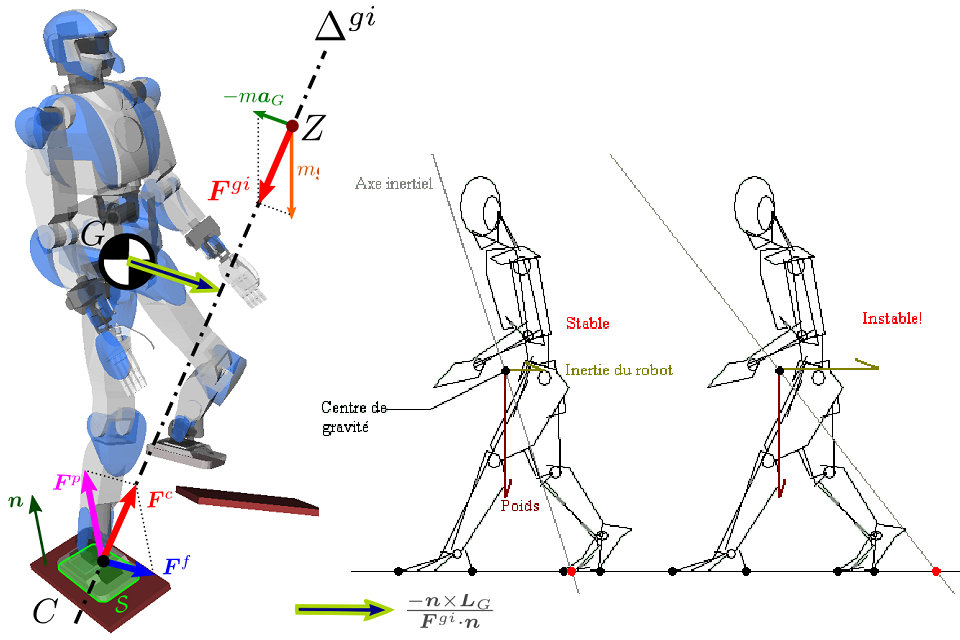
Die Abbildung rechts zeigt den Schwerpunkt  das Druckzentrum des Fuß-Rechts-Kontakts sowie ein ZMP  . Punkte  sind immer auf der Inertialachse ausgerichtet  . Letzteres passiert nicht unbedingt den Schwerpunkt, es sei denn, der Roboter behält seinen Drehimpuls (  ), was eine häufige Arbeitshypothese in der Fortbewegung ist.

Sonderfall von ebenem Boden
Solange der Kontakt mit der Oberfläche nicht bricht, befindet sich der Druckmittelpunkt notwendigerweise innerhalb der Kontaktfläche zwischen dem Roboter und der Umgebung. Wenn die beiden Füße des Roboters mit der gleichen Oberfläche (dem Boden) in Kontakt stehen, wird diese Oberfläche der Levitation  ist die konvexe Hülle aller Stützpunkte, dh die Menge der Punkte, die sich „zwischen den beiden Füßen“ befinden. Diese Oberfläche ermöglicht die Definition von Drücken und Reibung und damit eines zugehörigen Druckzentrums (weitere Informationen finden Sie unter Druckcenter). COP und ZMP stimmen überein, wir erhalten das Kriterium:

Nicht-Neigungskriterium: Während des neigungsfreien Betriebs befindet sich der ZMP innerhalb der Auftriebsfläche, definiert als konvexe Hülle der Drehpunkte.

Dieses Kriterium wird am häufigsten für das Laufen von humanoiden Robotern auf ebenem Boden verwendet.

Anwendungen
Der Nullmomentpunkt wurde als Messgröße vorgeschlagen, mit der die Stabilität gegen das Umkippen von Robotern wie dem iRobot PackBot beim Navigieren von Rampen und Hindernissen beurteilt werden kann.