Partikelkinematik ist die Untersuchung der Flugbahn eines Partikels. Die Position eines Partikels wird als Koordinatenvektor vom Ursprung eines Koordinatenrahmens bis zum Partikel definiert.

Kinematik einer Teilchenflugbahn in einem nicht rotierenden Bezugssystem
Im allgemeinsten Fall wird ein dreidimensionales Koordinatensystem verwendet, um die Position eines Partikels zu definieren. Wenn sich das Teilchen jedoch in einer Oberfläche bewegen muss, reicht ein zweidimensionales Koordinatensystem aus. Alle Beobachtungen in der Physik sind unvollständig, ohne dass diese Beobachtungen in Bezug auf einen Referenzrahmen beschrieben werden.

Der Positionsvektor eines Partikels ist ein Vektor, der vom Ursprung des Bezugsrahmens zum Partikel gezeichnet wird. Es drückt sowohl die Entfernung des Punktes vom Ursprung als auch seine Richtung vom Ursprung aus. In drei Dimensionen kann die Position des Punktes P als ausgedrückt werden 

woher  .  , und  sind die kartesischen Koordinaten und  .  und  sind die Einheitsvektoren entlang der  .  , und  Koordinatenachsen. Die Größe des Positionsvektors  gibt den Abstand zwischen dem Punkt an  und der Ursprung.

Der Richtungskosinus des Positionsvektors liefert ein quantitatives Richtungsmaß. Es ist wichtig zu beachten, dass der Positionsvektor eines Partikels nicht eindeutig ist. Der Positionsvektor eines gegebenen Partikels unterscheidet sich in Bezug auf verschiedene Referenzrahmen.

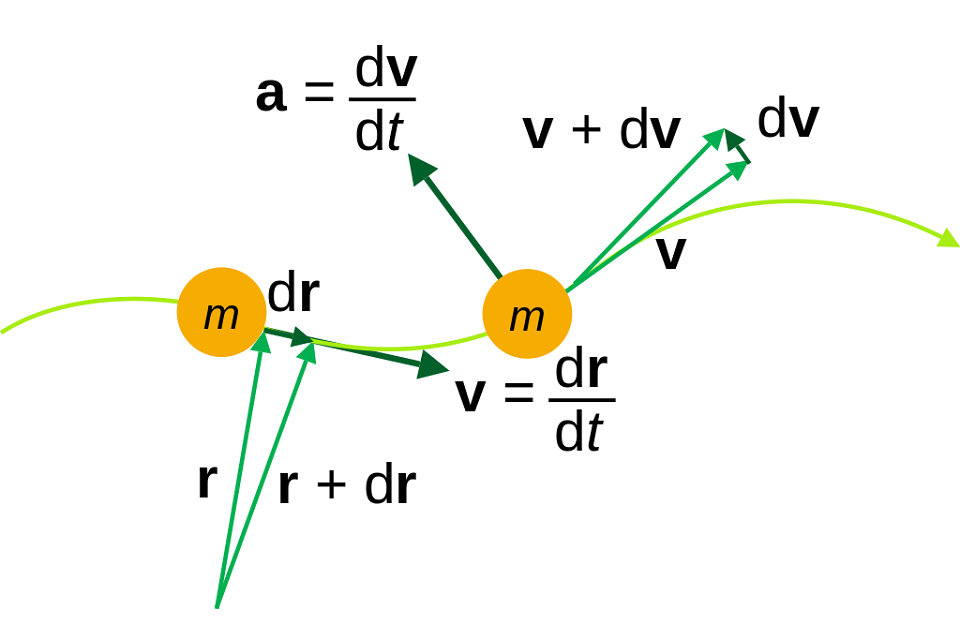
Die Flugbahn eines Partikels ist eine Vektorfunktion der Zeit.  , die die Kurve definiert, die von dem sich bewegenden Teilchen durch gegeben wird 
wobei die Koordinaten x _P , y _P und z _P jeweils Funktionen der Zeit sind.

Geschwindigkeit und Geschwindigkeit
Die Geschwindigkeit eines Partikels ist eine Vektorgröße, die die Bewegungsrichtung und die Größe der Bewegung des Partikels beschreibt. Mathematisch gesehen ist die Änderungsrate des Positionsvektors eines Punktes in Bezug auf die Zeit die Geschwindigkeit des Punktes. Betrachten Sie das Verhältnis, das durch Division der Differenz zweier Positionen eines Partikels durch das Zeitintervall gebildet wird. Dieses Verhältnis wird als Durchschnittsgeschwindigkeit in diesem Zeitintervall bezeichnet und ist definiert als Geschwindigkeit = Verschiebung / benötigte Zeit

Dabei ist ΔP die Änderung des Positionsvektors über dem Zeitintervall Δt.
Wenn die Zeitspanne Δt immer kleiner wird, wird die Durchschnittsgeschwindigkeit zur zeitlichen Ableitung des Positionsvektors. 

Die Geschwindigkeit eines Objekts ist die Größe | V | von seiner Geschwindigkeit. Es ist eine skalare Größe:

Dabei ist s die Bogenlänge, die entlang der Flugbahn des Partikels gemessen wird. Diese Bogenlänge, die ein Partikel im Laufe der Zeit zurücklegt, ist eine nicht abnehmende Größe. Daher ist ds / dt nicht negativ, was bedeutet, dass auch die Geschwindigkeit nicht negativ ist.

Beschleunigung
Der Geschwindigkeitsvektor kann sich in der Größe und in der Richtung oder in beiden gleichzeitig ändern. Daher ist die Beschleunigung die Änderungsrate der Größe des Geschwindigkeitsvektors plus die Änderungsrate des Richtungsvektors dieses Vektors. Die gleiche Überlegung, die in Bezug auf die Position eines Partikels zum Definieren der Geschwindigkeit verwendet wird, kann auf die Geschwindigkeit zum Definieren der Beschleunigung angewendet werden. Die Beschleunigung eines Partikels ist der Vektor, der durch die Änderungsrate des Geschwindigkeitsvektors definiert wird. Die durchschnittliche Beschleunigung eines Partikels über ein Zeitintervall wird als Verhältnis definiert.

Dabei ist ΔV die Differenz im Geschwindigkeitsvektor und Δt das Zeitintervall.
Die Beschleunigung des Partikels ist die Grenze der durchschnittlichen Beschleunigung, wenn sich das Zeitintervall gegen null bewegt, was die Zeitableitung ist. 
oder

Die Größe der Beschleunigung eines Objekts ist die Größe | A | seines Beschleunigungsvektors. Es ist eine skalare Größe:

Relativer Positionsvektor

das ist der Unterschied zwischen den Komponenten ihrer Positionsvektoren.

Wenn Punkt B Positionskomponenten hat 

dann ist die Position von Punkt A relativ zu Punkt B die Differenz zwischen ihren Komponenten: 

Relative Geschwindigkeit
Die Geschwindigkeit eines Punktes relativ zu einem anderen ist einfach die Differenz zwischen ihren Geschwindigkeiten

Das ist der Unterschied zwischen den Komponenten ihrer Geschwindigkeiten.
Wenn Punkt A Geschwindigkeitskomponenten hat 
und Punkt B hat Geschwindigkeitskomponenten 

dann ist die Geschwindigkeit von Punkt A relativ zu Punkt B die Differenz zwischen ihren Komponenten: 
Alternativ könnte das gleiche Ergebnis durch Berechnen der zeitlichen Ableitung des relativen Positionsvektors R _{B / A erhalten werden} .

In dem Fall, in dem die Geschwindigkeit nahe an der Lichtgeschwindigkeit c liegt (im Allgemeinen innerhalb von 95%), wird ein anderes Schema der Relativgeschwindigkeit, Geschwindigkeit genannt, das von dem Verhältnis von V zu c abhängt, in besonderer Relativitätstheorie verwendet.

Relative Beschleunigung
Die Beschleunigung eines Punktes C relativ zu einem anderen Punkt B ist einfach die Differenz zwischen ihren Beschleunigungen.

Das ist der Unterschied zwischen den Komponenten ihrer Beschleunigungen.
Wenn Punkt C Beschleunigungskomponenten hat 
und Punkt B hat Beschleunigungskomponenten 

dann ist die Beschleunigung von Punkt C relativ zu Punkt B die Differenz zwischen ihren Komponenten: 
Alternativ könnte das gleiche Ergebnis erhalten werden, indem die zweite Zeitableitung des relativen Positionsvektors PB _{/ A} berechnet wird.

Teilchenbahnen unter konstanter Beschleunigung
Für den Fall einer konstanten Beschleunigung kann die Differentialgleichung Eq 1) integriert werden, da der Beschleunigungsvektor A eines Punktes P in Betrag und Richtung konstant ist. Ein solcher Punkt soll eine gleichmäßig beschleunigte Bewegung erfahren ^{. In diesem Fall kann die Geschwindigkeit V (t) und dann die Trajektorie P (t) des Partikels durch Integrieren der Beschleunigungsgleichung A in Bezug auf die Zeit erhalten werden.}

Angenommen, die Anfangsbedingungen der Position,  und Geschwindigkeit  zum Zeitpunkt  bekannt sind, ergibt die erste Integration die Geschwindigkeit des Partikels als Funktion der Zeit.

Eine zweite Integration ergibt ihren Weg (Flugbahn),

Zusätzliche Beziehungen zwischen Verschiebung, Geschwindigkeit, Beschleunigung und Zeit können abgeleitet werden. Da die Beschleunigung konstant ist, kann in die obige Gleichung eingesetzt werden, um zu ergeben:

Eine Beziehung zwischen Geschwindigkeit, Position und Beschleunigung ohne explizite Zeitabhängigkeit kann durch Lösen der durchschnittlichen Beschleunigung für die Zeit und Ersetzen und Vereinfachen erhalten werden

Dabei bezeichnet the das Punktprodukt, was angemessen ist, da die Produkte eher Skalare als Vektoren sind.

Der Punkt kann durch den Cosinus des Winkels ersetzt werden  zwischen den Vektoren ^{und den Vektoren nach ihrer Größe, in diesem Fall:}

Bei Beschleunigung immer in Bewegungsrichtung liegt der Winkel zwischen den Vektoren (  ) ist 0, also  , und 

Dies kann durch die Notation für die Beträge der Vektoren vereinfacht werden  ^{woher  kann ein beliebiger kurvenreicher Pfad sein, wenn die konstante tangentiale Beschleunigung entlang diesem Pfad angewendet wird , so} 

Dies reduziert die parametrischen Bewegungsgleichungen des Partikels auf eine kartesische Beziehung zwischen Geschwindigkeit und Position. Diese Beziehung ist nützlich, wenn die Zeit unbekannt ist. Das wissen wir auch  oder  ist der Bereich unter av, t graph. Wir können nehmen  indem Sie den oberen Bereich und den unteren Bereich hinzufügen. Der untere Bereich ist ein Rechteck und der Bereich eines Rechtecks ​​ist der woher  ist die Breite und  ist die Höhe In diesem Fall  und  (Notiere dass der  Hier unterscheidet sich die Beschleunigung  ). Dies bedeutet, dass der untere Bereich ist  . Finden wir nun den oberen Bereich (ein Dreieck). Die Fläche eines Dreiecks ist  woher  ist die Basis und  ist die Höhe. In diesem Fall  &  oder  . Hinzufügen  und  ergibt die Gleichung  ergibt die Gleichung  . Diese Gleichung ist sehr nützlich bei der Endgeschwindigkeit  ist unbekannt.

Teilchenbahnen in zylindrisch-polaren Koordinaten
Es ist oft praktisch, die Flugbahn eines Partikels P (t) = (X (t), Y (t) und Z (t)) unter Verwendung von Polarkoordinaten in der X-Y-Ebene zu formulieren. In diesem Fall haben Geschwindigkeit und Beschleunigung eine bequeme Form.

Es sei daran erinnert, dass die Flugbahn eines Partikels P durch seinen Koordinatenvektor P definiert ist, der in einem festen Bezugsrahmen F gemessen wird. Wenn sich der Partikel bewegt, folgt sein Koordinatenvektor P (t) seiner Trajektorie, die eine Kurve im Raum ist, die gegeben ist durch:

Dabei sind i, j und k die Einheitsvektoren entlang der X-, Y- und Z-Achse des Referenzrahmens F.

Betrachten wir ein Teilchen P, das sich nur auf der Oberfläche eines Kreiszylinders R (t) = konstant bewegt, ist es möglich, die Z-Achse des festen Rahmens F mit der Zylinderachse auszurichten.Dann kann der Winkel θ um diese Achse in der X-Y-Ebene verwendet werden, um die Trajektorie zu definieren als 

Die Zylinderkoordinaten für P (t) können durch Einführung der radialen und tangentialen Einheitsvektoren vereinfacht werden. 

und ihre zeitlichen Ableitungen von der Elementarrechnung:



 .

Mit dieser Notation nimmt P (t) die Form an,

wobei R konstant ist, wenn sich das Teilchen nur auf der Oberfläche eines Zylinders mit Radius R bewegt.

Im Allgemeinen ist die Flugbahn P (t) nicht auf einen Kreiszylinder zu legen, so dass der Radius R mit der Zeit variiert und die Flugbahn des Teilchens in zylindrisch-polaren Koordinaten zu:

Wo R, Theta und Z kontinuierlich differenzierbare Funktionen der Zeit sein könnten und die Funktionsnotation der Einfachheit halber weggelassen wird. Der Geschwindigkeitsvektor V _P ist die zeitliche Ableitung der Trajektorie P (t), die ergibt:  .

In ähnlicher Weise ist die Beschleunigung A _P , die die zeitliche Ableitung der Geschwindigkeit V _Pist, gegeben durch: 

Der Begriff  Wirkt in Richtung des Krümmungszentrums des Pfads an diesem Punkt auf dem Pfad, wird im Allgemeinen als Zentripetalbeschleunigung bezeichnet. Der Begriff  wird die Coriolis-Beschleunigung genannt.

Konstanter Radius
Wenn die Flugbahn des Partikels auf einem Zylinder liegen muss, dann ist der Radius R konstant und die Geschwindigkeits- und Beschleunigungsvektoren vereinfachen sich. Die Geschwindigkeit von V _P ist die zeitliche Ableitung der Flugbahn P (t).

Der Beschleunigungsvektor wird zu:

Planare kreisförmige Flugbahnen
Ein spezieller Fall einer Teilchenbahn auf einem Kreiszylinder tritt auf, wenn sich entlang der Z-Achse keine Bewegung befindet:

wobei R und Z ₀ Konstanten sind. In diesem Fall ist die Geschwindigkeit V _P gegeben durch:

woher

ist die Winkelgeschwindigkeit des Einheitsvektors _eθ um die z-Achse des Zylinders.
Die Beschleunigung A _P des Partikels P ist nun gegeben durch:

Die Komponenten

werden als radiale und tangentiale Komponenten der Beschleunigung bezeichnet.
Die Notation für Winkelgeschwindigkeit und Winkelbeschleunigung wird häufig als definiert

So werden auch die radialen und tangentialen Beschleunigungskomponenten für Kreisbahnen geschrieben

Zeigen Sie Flugbahnen in einem Körper, der sich in der Ebene bewegt

Matrixdarstellung
Die Kombination von Rotation und Translation in der Ebene R ² kann durch einen bestimmten Typ von ³ × ^3- Matrix dargestellt werden, der als homogene Transformation bezeichnet wird. Die homogene 3×3-Transformation ist aus einer 2×2-Rotationsmatrix A (φ) und dem 2×1-Translationsvektor d = (d _x , d _y ) aufgebaut: 

Diese homogenen Transformationen führen starre Transformationen an den Punkten in der Ebene z = 1 durch, dh an Punkten mit den Koordinaten p = (x, y, 1).

Insbesondere soll p die Koordinaten von Punkten in einem Referenzrahmen M definieren, der mit einem festen Rahmen F zusammenfällt. Wenn der Ursprung von M um den Translationsvektor d relativ zu dem Ursprung von F verschoben wird und um den Winkel φ relativ zu dem gedreht wird x-Achse von F, die neuen Koordinaten in F von Punkten in M ​​sind gegeben durch:

Homogene Transformationen repräsentieren affine Transformationen. Diese Formulierung ist notwendig, da eine Translation keine lineare Transformation von R ^{2 ist} . Durch die Verwendung der projektiven Geometrie, so dass R ² als eine Teilmenge von R ^{3 betrachtet wird} , werden Translations zu affinen linearen Transformationen.

Reine Übersetzung
Wenn sich ein starrer Körper so bewegt, dass sich sein Referenzrahmen M relativ zu dem festen Rahmen F nicht dreht (∅ = 0), wird die Bewegung als reine Translation bezeichnet. In diesem Fall ist die Flugbahn jedes Punktes im Körper ein Versatz der Flugbahn d (t) des Ursprungs von M, d. H. 

Somit sind für Körper in reiner Translation die Geschwindigkeit und Beschleunigung jedes Punktes P im Körper gegeben durch: 

wobei der Punkt die Ableitung in Bezug auf die Zeit bezeichnet und V ₀ und A ₀ die Geschwindigkeit bzw. Beschleunigung des Ursprungs des sich bewegenden Rahmens M sind. Es sei daran erinnert, dass der Koordinatenvektor p in M ​​konstant ist, so dass seine Ableitung Null ist.

Drehung eines Körpers um eine feste Achse
Rotations- oder Winkelkinematik ist die Beschreibung der Rotation eines Objekts. Die Beschreibung der Rotation erfordert eine Methode zur Beschreibung der Orientierung. Übliche Beschreibungen umfassen Euler-Winkel und die Kinematik von Windungen, die durch algebraische Produkte induziert werden.

Im Folgenden beschränkt sich die Aufmerksamkeit auf die einfache Drehung um eine Achse mit fester Orientierung. Die Z-Achse wurde zur Vereinfachung gewählt.

Position
Dies ermöglicht die Beschreibung einer Drehung als Winkelposition eines planaren Referenzrahmens M relativ zu einem festen F um diese gemeinsame z-Achse. Die Koordinaten p = (x, y) in M ​​beziehen sich auf die Koordinaten P = (X, Y) in F durch die Matrixgleichung:

woher

ist die Rotationsmatrix, die die Winkelposition von M relativ zu F als Funktion der Zeit definiert.

Geschwindigkeit
Wenn sich der Punkt p nicht in M ​​bewegt, ist seine Geschwindigkeit in F durch gegeben

Es ist zweckmäßig, die Koordinaten p zu eliminieren und dies als eine Operation auf die Trajektorie P (t) zu schreiben. 

wo die Matrix

ist als Winkelgeschwindigkeitsmatrix von M relativ zu F bekannt. Der Parameter ω ist die zeitliche Ableitung des Winkels θ, das heißt:

Beschleunigung
Die Beschleunigung von P (t) in F wird als zeitliche Ableitung der Geschwindigkeit erhalten.

was wird

woher

ist die Winkelbeschleunigungsmatrix von M auf F und

Die Beschreibung der Rotation umfasst dann diese drei Größen:

Winkelposition: Der orientierte Abstand von einem ausgewählten Ursprung auf der Rotationsachse zu einem Punkt eines Objekts ist ein Vektor r (t), der den Punkt lokalisiert. Der Vektor r (t) hat eine Projektion (oder äquivalent eine Komponente) r _⊥ (t) auf einer Ebene senkrecht zur Drehachse.Dann ist die Winkelposition dieses Punktes der Winkel θ von einer Bezugsachse (typischerweise der positiven x-Achse) zu dem Vektor r _⊥ (t) in einem bekannten Rotationssinn (typischerweise durch die_{Rechtshandregel} gegeben).

Winkelgeschwindigkeit: Die Winkelgeschwindigkeit ω ist die Geschwindigkeit, mit der sich die Winkelposition θ in Bezug auf die Zeit t ändert.

Die Winkelgeschwindigkeit ist in Fig. 1 durch einen entlang der Drehachse zeigenden Vektor Ω dargestellt, wobei die Größe ω und die Richtung durch die Drehrichtung bestimmt werden, wie sie durch die Rechtsregel gegeben ist.

Winkelbeschleunigung: Die Größe der Winkelbeschleunigung α ist die Rate, mit der sich die Winkelgeschwindigkeit ω in Bezug auf die Zeit t ändert:

Die Gleichungen der Translationskinematik lassen sich leicht auf eine planare Rotationskinematik für konstante Winkelbeschleunigung mit einfachem Variablenaustausch erweitern:

Hier sind θi bzw. θf die Anfangs- und Endwinkelpositionen, ωi und ωf sind die Anfangs- und Endwinkelgeschwindigkeiten und α ist die konstante Winkelbeschleunigung. Obwohl die Position im Raum und die Geschwindigkeit im Raum beide echte Vektoren sind (hinsichtlich ihrer Eigenschaften unter Drehung), ist der Winkel selbst ebenso wie die Winkelgeschwindigkeit kein wahrer Vektor.

Punktewege im Körper bewegen sich in drei Dimensionen
Wichtige Formeln in der Kinematik definieren die Geschwindigkeit und Beschleunigung von Punkten in einem sich bewegenden Körper, wenn sie Trajektorien im dreidimensionalen Raum verfolgen.Dies ist besonders wichtig für den Massenmittelpunkt eines Körpers, der dazu verwendet wird, Bewegungsgleichungen unter Verwendung entweder des zweiten Newtonschen Gesetzes oder der Lagrange-Gleichung abzuleiten.

Position
Um diese Formeln zu definieren, wird die Bewegung einer Komponente B eines mechanischen Systems durch die Menge der Rotationen [A (t)] und die in der homogenen Transformation [T (t)] gebildeten Translationen d (t) = [A] definiert (t), d (t)]. Wenn p die Koordinaten eines Punktes P in B ist, die in dem sich bewegenden Bezugsrahmen M gemessen werden, dann ist die in F verfolgte Flugbahn dieses Punktes gegeben durch 

Diese Notation unterscheidet nicht zwischen P = (X, Y, Z, 1) und P = (X, Y, Z), was im Kontext hoffentlich klar ist.
Diese Gleichung für die Trajektorie von P kann invertiert werden, um den Koordinatenvektor p in M ​​zu berechnen: 

Dieser Ausdruck verwendet die Tatsache, dass die Transponierte einer Rotationsmatrix auch ihre Umkehrung ist, d. H.

Geschwindigkeit
Die Geschwindigkeit des Punktes P entlang seiner Trajektorie P (t) wird als zeitliche Ableitung dieses Positionsvektors erhalten. 

Der Punkt bezeichnet die Ableitung in Bezug auf die Zeit; Da p konstant ist, ist seine Ableitung gleich Null.

Diese Formel kann modifiziert werden, um die Geschwindigkeit von P zu erhalten, indem auf ihrer im festen Rahmen F gemessenen Trajektorie P (t) gearbeitet wird. Das Ersetzen der inversen Transformation von p in die Geschwindigkeitsgleichung ergibt: 

Die Matrix [S] ist gegeben durch:

woher

ist die Winkelgeschwindigkeitsmatrix.

Multipliziert mit dem Operator [S] erhält die Formel für die Geschwindigkeit V _P die Form:

wobei der Vektor ω der Winkelgeschwindigkeitsvektor ist, der aus den Komponenten der Matrix [Ω] erhalten wird; der Vektor

ist die Position von P relativ zum Ursprung O des sich bewegenden Rahmens M; und

ist die Geschwindigkeit des Ursprungs O.

Beschleunigung
Die Beschleunigung eines Punktes P in einem sich bewegenden Körper B ergibt sich als zeitliche Ableitung seines Geschwindigkeitsvektors: 

Diese Gleichung kann zunächst durch Berechnung erweitert werden

und

Die Formel für die Beschleunigung A _P kann nun erhalten werden als:

oder

wobei α der Winkelbeschleunigungsvektor ist, der aus der Ableitung der Winkelgeschwindigkeitsmatrix erhalten wird;

ist der relative Positionsvektor (die Position von P relativ zum Ursprung O des sich bewegenden Rahmens M); und

ist die Beschleunigung des Ursprungs des beweglichen Rahmens M.