Cinemática de partículas é o estudo da trajetória de uma partícula. A posição de uma partícula é definida como o vetor de coordenadas desde a origem de um quadro de coordenadas até a partícula.
Cinemática de uma trajetória de partículas em um referencial não rotativo
No caso mais geral, um sistema de coordenadas tridimensional é usado para definir a posição de uma partícula. No entanto, se a partícula for restrita a se mover em uma superfície, um sistema de coordenadas bidimensional é suficiente. Todas as observações em física são incompletas sem que essas observações sejam descritas em relação a um referencial.
O vetor de posição de uma partícula é um vetor desenhado a partir da origem do quadro de referência para a partícula. Ela expressa tanto a distância do ponto da origem quanto sua direção a partir da origem. Em três dimensões, a posição do ponto P pode ser expressa como
Onde 










Os cossenos de direção do vetor de posição fornecem uma medida quantitativa de direção. É importante notar que o vetor de posição de uma partícula não é único. O vetor de posição de uma dada partícula é diferente em relação a diferentes quadros de referência.
A trajetória de uma partícula é uma função vetorial do tempo, 
onde as coordenadas x P , y P ez P são funções do tempo.
Velocidade e velocidade
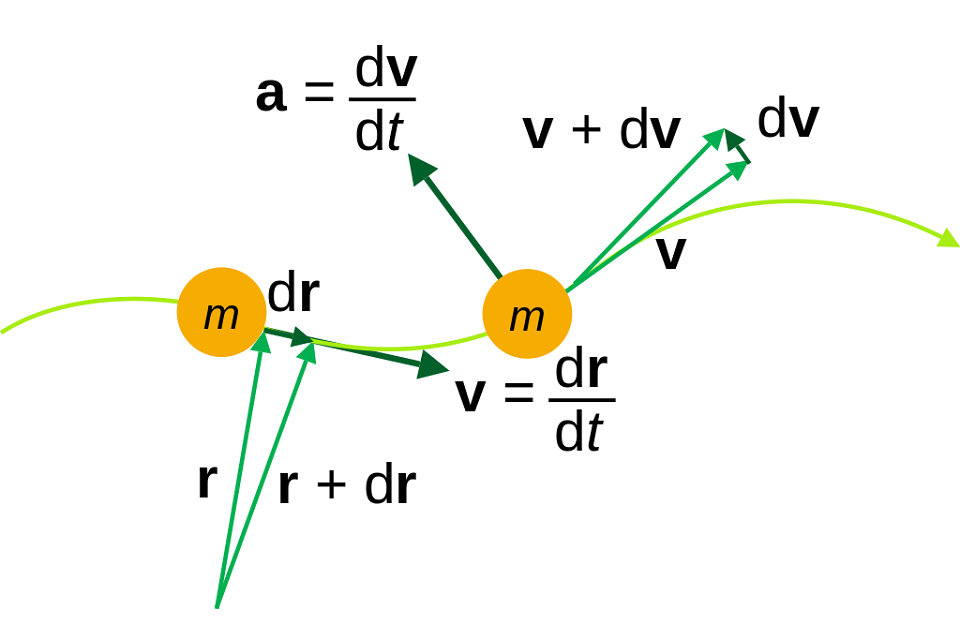
A velocidade de uma partícula é uma grandeza vetorial que descreve a direção do movimento e a magnitude do movimento da partícula. Mais matematicamente, a taxa de mudança do vetor de posição de um ponto, em relação ao tempo, é a velocidade do ponto. Considere a proporção formada dividindo a diferença de duas posições de uma partícula pelo intervalo de tempo. Essa relação é chamada de velocidade média ao longo desse intervalo de tempo e é definida como Velocidade = deslocamento / tempo gasto
onde ΔP é a mudança no vetor de posição ao longo do intervalo de tempo Δt.
No limite à medida que o intervalo de tempo Δt se torna menor e menor, a velocidade média torna-se a derivada de tempo do vetor de posição,
A velocidade de um objeto é a magnitude | V | da sua velocidade. É uma quantidade escalar:
onde s é o comprimento do arco medido ao longo da trajetória da partícula. Este comprimento de arco percorrido por uma partícula ao longo do tempo é uma quantidade não decrescente. Portanto, ds / dt é não-negativo, o que implica que a velocidade também é não-negativa.
Aceleração
O vetor de velocidade pode mudar em magnitude e direção ou ambos ao mesmo tempo. Portanto, a aceleração é a taxa de mudança da magnitude do vetor de velocidade mais a taxa de mudança de direção daquele vetor. O mesmo raciocínio usado com relação à posição de uma partícula para definir a velocidade pode ser aplicado à velocidade para definir a aceleração. A aceleração de uma partícula é o vetor definido pela taxa de variação do vetor de velocidade. A aceleração média de uma partícula ao longo de um intervalo de tempo é definida como a razão.
onde ΔV é a diferença no vetor de velocidade e Δt é o intervalo de tempo.
A aceleração da partícula é o limite da aceleração média à medida que o intervalo de tempo se aproxima de zero, que é a derivada de tempo,
ou
A magnitude da aceleração de um objeto é a magnitude | A | do seu vetor de aceleração. É uma quantidade escalar:
Vetor de posição relativa
qual é a diferença entre os componentes de seus vetores de posição.
Se o ponto B tiver componentes de posição
então a posição do ponto A em relação ao ponto B é a diferença entre seus componentes:
Velocidade relativa
A velocidade de um ponto em relação ao outro é simplesmente a diferença entre suas velocidades
qual é a diferença entre os componentes de suas velocidades.
Se o ponto A tiver componentes de velocidade
e o ponto B tem componentes de velocidade
então a velocidade do ponto A em relação ao ponto B é a diferença entre seus componentes:
Alternativamente, este mesmo resultado pode ser obtido calculando a derivada de tempo do vetor de posição relativo R B / A.
No caso em que a velocidade é próxima da velocidade da luz c (geralmente dentro de 95%), outro esquema de velocidade relativa chamado de rapidez, que depende da relação de V para c, é usado na relatividade especial.
Aceleração relativa
A aceleração de um ponto C em relação a outro ponto B é simplesmente a diferença entre suas acelerações.
qual é a diferença entre os componentes de suas acelerações.
Se o ponto C tiver componentes de aceleração
e o ponto B tem componentes de aceleração
então a aceleração do ponto C em relação ao ponto B é a diferença entre seus componentes:
Alternativamente, este mesmo resultado pode ser obtido calculando a segunda derivada temporal do vetor de posição relativa PB / A.
Trajetórias de partículas sob aceleração constante
Para o caso de aceleração constante, a equação diferencial Eq 1) pode ser integrada, pois o vetor de aceleração A de um ponto P é constante em magnitude e direção. Diz-se que tal ponto sofre um movimento uniformemente acelerado . Neste caso, a velocidade V (t) e, em seguida, a trajetória P (t) da partícula pode ser obtida integrando a equação de aceleração A em relação ao tempo.
Assumindo que as condições iniciais da posição, 


Uma segunda integração produz seu caminho (trajetória),
Relações adicionais entre deslocamento, velocidade, aceleração e tempo podem ser derivadas.Como a aceleração é constante, 
Uma relação entre velocidade, posição e aceleração sem dependência de tempo explícita pode ser obtida resolvendo a aceleração média do tempo e substituindo e simplificando
onde ∘ denota o produto escalar, o que é apropriado, pois os produtos são escalares e não vetores.
O ponto pode ser substituído pelo cosseno do ângulo 
No caso de aceleração sempre na direção do movimento, o ângulo entre os vetores ( 

Isso pode ser simplificado usando a notação para as magnitudes dos vetores 

Isso reduz as equações paramétricas de movimento da partícula para uma relação cartesiana de velocidade versus posição. Essa relação é útil quando o tempo é desconhecido. Nós também sabemos que 





















Trajetórias de partículas em coordenadas cilíndrico-polares
Geralmente é conveniente formular a trajetória de uma partícula P (t) = (X (t), Y (t) e Z (t)) usando coordenadas polares no plano X – Y. Nesse caso, sua velocidade e aceleração assumem uma forma conveniente.
Lembre-se que a trajetória de uma partícula P é definida por seu vetor coordenado P medido em um referencial fixo F. À medida que a partícula se move, seu vetor coordenado P (t) traça sua trajetória, que é uma curva no espaço, dada por:
onde i, jek são os vetores unitários ao longo dos eixos X, Y e Z do referencial F, respectivamente.
Considere uma partícula P que se move apenas na superfície de um cilindro circular R (t) = constante, é possível alinhar o eixo Z da estrutura fixa F com o eixo do cilindro. Então, o ângulo θ em torno deste eixo no plano X-Y pode ser usado para definir a trajetória como,
As coordenadas cilíndricas de P (t) podem ser simplificadas pela introdução dos vetores unitários radiais e tangenciais,
e seus derivados temporais do cálculo elementar:

Usando esta notação, P (t) assume a forma,
onde R é constante no caso de a partícula se mover apenas na superfície de um cilindro de raio R.
Em geral, a trajetória P (t) não é restrita a ficar em um cilindro circular, então o raio R varia com o tempo e a trajetória da partícula em coordenadas polares-cilíndricas se torna:
Onde R, theta e Z podem ser funções continuamente diferenciadas do tempo e a notação de função é descartada para simplificar. O vetor velocidade V P é a derivada temporal da trajetória P (t), que produz: 
Da mesma forma, a aceleração A P , que é a derivada de tempo da velocidade V P , é dada por:
O termo 

Raio Constante
Se a trajetória da partícula for limitada a ficar em um cilindro, então o raio R é constante e os vetores de velocidade e aceleração se simplificam. A velocidade de V P é a derivada temporal da trajetória P (t),
O vetor de aceleração se torna:
Trajetórias circulares planas
Um caso especial de uma trajetória de partículas em um cilindro circular ocorre quando não há movimento ao longo do eixo Z:
onde R e Z 0 são constantes. Neste caso, a velocidade V P é dada por:
Onde
é a velocidade angular do vetor unitário e θ em torno do eixo z do cilindro.
A aceleração A P da partícula P é agora dada por:
Os componentes
são chamados, respectivamente, os componentes radiais e tangenciais da aceleração.
A notação para velocidade angular e aceleração angular é geralmente definida como
então os componentes de aceleração radial e tangencial para trajetórias circulares também são escritos como
Trajetórias de ponto em um corpo que se move no plano
Representação matricial
A combinação de uma rotação e translação no plano R2 pode ser representada por um certo tipo de matriz 3×3 conhecida como uma transformação homogênea. A transformada homogênea 3×3 é construída a partir de uma matriz de rotação 2×2 A (φ) e o vetor de translação 2×1 d = (d x , d y ), como:
Estas transformações homogêneas realizam transformações rígidas nos pontos no plano z = 1, que é em pontos com coordenadas p = (x, y, 1).
Em particular, vamos p definir as coordenadas dos pontos em um quadro de referência M coincidente com um quadro fixo F. Então, quando a origem de M é deslocada pelo vetor de translação d relativo à origem de Fand girada pelo ângulo φ em relação ao eixo x de F, as novas coordenadas em F de pontos em M são dadas por:
Transformações homogêneas representam transformações afins. Esta formulação é necessária porque uma tradução não é uma transformação linear de R2. No entanto, usando a geometria projetiva, de modo que R2 é considerado um subconjunto de R3, as traduções tornam-se transformações lineares afim.
Tradução pura
Se um corpo rígido se move de modo que o seu quadro de referência M não gira (∅ = 0) em relação ao quadro fixo F, o movimento é chamado de translação pura. Nesse caso, a trajetória de cada ponto no corpo é um deslocamento da trajetória d (t) da origem de M, ou seja:
Assim, para corpos em tradução pura, a velocidade e aceleração de cada ponto P no corpo são dadas por:
onde o ponto denota a derivada em relação ao tempo e V O e A O são a velocidade e aceleração, respectivamente, da origem da trama móvel M. Lembre-se de que o vetor de coordenadas p em M é constante, portanto sua derivada é zero.
Rotação de um corpo em torno de um eixo fixo
Cinemática rotacional ou angular é a descrição da rotação de um objeto. A descrição da rotação requer algum método para descrever a orientação. Descrições comuns incluem ângulos de Euler e a cinemática das voltas induzidas por produtos algébricos.
No que se segue, a atenção é restrita à simples rotação em torno de um eixo de orientação fixa. O eixo z foi escolhido por conveniência.
Posição
Isto permite a descrição de uma rotação como a posição angular de um referencial planar M em relação a um F fixo sobre este eixo z compartilhado. As coordenadas p = (x, y) em M estão relacionadas com as coordenadas P = (X, Y) em F pela equação matricial:
Onde
é a matriz de rotação que define a posição angular de M em relação a F como uma função do tempo.
Velocidade
Se o ponto p não se move em M, sua velocidade em F é dada por
É conveniente eliminar as coordenadas p e escrever isto como uma operação na trajetória P (t),
onde a matriz
é conhecido como a matriz de velocidade angular de M em relação a F. O parâmetro ω é a derivada temporal do ângulo θ, ou seja:
Aceleração
A aceleração de P (t) em F é obtida como a derivada temporal da velocidade,
que se torna
Onde
é a matriz de aceleração angular de M em F, e
A descrição da rotação envolve então estas três quantidades:
Posição angular: a distância orientada de uma origem selecionada no eixo rotacional até um ponto de um objeto é um vetor r (t) localizando o ponto. O vetor r (t) tem alguma projeção (ou, equivalentemente, algum componente) r ⊥ (t) em um plano perpendicular ao eixo de rotação. Então a posição angular desse ponto é o ângulo θ de um eixo de referência (tipicamente o eixo x positivo) para o vetor r ⊥ (t) em um sentido de rotação conhecido (tipicamente dado pela regra da mão direita).
Velocidade angular: a velocidade angular ω é a taxa na qual a posição angular θ muda em relação ao tempo t:
A velocidade angular é representada na Figura 1 por um vetor Ω apontando ao longo do eixo de rotação com magnitude ω e sentido determinado pelo sentido de rotação dado pela regra da mão direita.
Aceleração angular: a magnitude da aceleração angular α é a taxa na qual a velocidade angular ω muda em relação ao tempo t:
As equações da cinemática translacional podem ser facilmente estendidas à cinemática rotacional planar para aceleração angular constante com trocas de variáveis simples:
Aqui θ i e θ f são, respectivamente, as posições angulares inicial e final, ω i e ω f são, respectivamente, as velocidades angulares iniciais e finais, e α é a aceleração angular constante.Embora a posição no espaço e a velocidade no espaço sejam ambos vetores verdadeiros (em termos de suas propriedades sob rotação), assim como a velocidade angular, o próprio ângulo não é um vetor verdadeiro.
Trajetórias de pontos no corpo em movimento em três dimensões
Fórmulas importantes na cinemática definem a velocidade e a aceleração de pontos em um corpo em movimento à medida que traçam trajetórias no espaço tridimensional. Isso é particularmente importante para o centro de massa de um corpo, que é usado para derivar equações de movimento usando a segunda lei de Newton ou as equações de Lagrange.
Posição
Para definir estas fórmulas, o movimento de um componente B de um sistema mecânico é definido pelo conjunto de rotações [A (t)] e translações d (t) montadas na transformação homogênea [T (t)] = [A (t), d (t)]. Se p é a coordenada de um ponto P em B medido no referencial móvel M, então a trajetória deste ponto traçada em F é dada por:
Essa notação não distingue entre P = (X, Y, Z, 1) e P = (X, Y, Z), o que esperamos ser claro no contexto.
Esta equação para a trajetória de P pode ser invertida para calcular o vetor de coordenadas p em M como:
Essa expressão usa o fato de que a transposição de uma matriz de rotação é também seu inverso, isto é:
Velocidade
A velocidade do ponto P ao longo de sua trajetória P (t) é obtida como a derivada temporal desse vetor de posição,
O ponto denota a derivada em relação ao tempo; porque p é constante, sua derivada é zero.
Esta fórmula pode ser modificada para obter a velocidade de P operando em sua trajetória P (t) medida no quadro fixo F. Substituindo a transformação inversa por p na equação de velocidade, obtém-se:
A matriz [S] é dada por:
Onde
é a matriz de velocidade angular.
Multiplicando pelo operador [S], a fórmula para a velocidade V P toma a forma:
onde o vetor ω é o vetor de velocidade angular obtido a partir dos componentes da matriz [Ω]; o vetor
é a posição de P em relação à origem O da estrutura móvel M; e
é a velocidade da origem O.
Aceleração
A aceleração de um ponto P em um corpo móvel B é obtida como a derivada temporal de seu vetor de velocidade:
Esta equação pode ser expandida em primeiro lugar computando
e
A fórmula para a aceleração A P agora pode ser obtida como:
ou
onde α é o vetor de aceleração angular obtido a partir da derivada da matriz de velocidade angular;
é o vetor de posição relativa (a posição de P em relação à origem O da estrutura móvel M); e
é a aceleração da origem do quadro móvel M.