Constante solaire – HiSoUR Art Culture Histoire

La constante solaire est une densité de flux mesurant le rayonnement électromagnétique solaire moyen (rayonnement solaire) par unité de surface. Il est mesuré sur une surface perpendiculaire aux rayons, une unité astronomique (AU) du Soleil (à peu près la distance du Soleil à la Terre).

La constante solaire comprend tous les types de rayonnement solaire, pas seulement la lumière visible. Il est mesuré par satellite à 1,361 kilowatts par mètre carré (kW / m²) au minimum solaire et environ 0,1% supérieur (environ 1,362 kW / m²) au maximum solaire.

La « constante » solaire n’est pas une constante physique au sens scientifique moderne de CODATA;c’est-à-dire que ce n’est pas comme la constante de Planck ou la vitesse de la lumière qui sont absolument constantes en physique. La constante solaire est une moyenne d’une valeur variable. Au cours des 400 dernières années, il a varié de moins de 0,2%.

Formule
Pour calculer la constante solaire, il suffit de diviser le flux d’énergie que le soleil émet par le rapport des surfaces entre la surface du soleil. $r_ {s} \,$ (la radio solaire) et celle d’une sphère radio $a_ {0} \$ (une unité astronomique) de celui-ci. Pour obtenir cette valeur qui, en pratique, est mesurée par des satellites, il faut l’utiliser comme température efficace $T {{{mathrm {eff}}}}$ ) Del Sol 5776 la valeur K.
${\ displaystyle K = \ sigma \ cdot T _ {\ mathrm {eff}} ^ {4} \ cdot ({\ frac {r_ {s}} {a_ {0}}}) ^ {2} = 1366 \ W \ cdot {m ^ {- 2}}}$
La constante solaire peut être exprimée en ${\ frac {calorias} {cm ^ {2} \ cdot minute}} \$ . Pour ce faire, rappelez-vous 1 juillet = 0,24 calories, 1 minute = 60 s et 1 m ² = 10 ⁴ cm ²
$K = 1366 {\ frac {joules} {s \ cdot m ^ {2}} = {\ frac {1366 \ cdot 0,24 \ cdot 60} {10 ^ {4}}} = 1,967 {\ frac {calories}} { cm ^ {2} \ cdot minute}} \ approx 2 {\ frac {calorias} {cm ^ {2} \ cdot minute}} \$ .
Une unité très utilisée pour mesurer l’énergie qui atteint le sommet de l’atmosphère en une journée est:
$1langley = 1 {\ frac {caloria} {cm ^ {2}}} \$

Ainsi un lieu à 30º de latitude nord reçoit le 21 juin, jour du solstice d’été, une insolation de 1004,7 langleys / jour et le 21 décembre, jour du solstice d’hiver seulement 480,4 langleys / jour.

Par ailleurs, l’insolation annuelle dans la partie supérieure de l’atmosphère à différentes latitudes peut être calculée. Pour le pôle, l’ensoleillement annuel est de 133,2 kilolangle / an tandis qu’à l’équateur il atteint 320,9 kilolangle / an où le klangley = 1000 langleys.

Calcul
L’irradiation solaire est mesurée par satellite au-dessus de l’atmosphère terrestre et est ensuite ajustée à l’aide de la loi du carré inverse pour déduire l’ampleur de l’éclairement solaire à une unité astronomique (UA) afin d’évaluer la constante solaire. La valeur moyenne approximative citée, 1,3608 ± 0,0005 kW / m², soit 81,65 kJ / m² par minute, équivaut à environ 1 951 calories par minute par centimètre carré, soit 1 951 langle par minute.

La production solaire est presque, mais pas tout à fait constante. Les variations de l’irradiance solaire totale (TSI) étaient petites et difficiles à détecter avec précision avec la technologie disponible avant l’ère du satellite (± 2% en 1954). La production solaire totale est maintenant mesurée comme étant variable (au cours des trois derniers cycles de taches solaires de 11 ans) d’environ 0,1%; voir la variation solaire pour plus de détails.

Luminosité solaire
l’énergie est appelée l’énergie émise par le soleil dans l’unité de temps. Par conséquent, il vaut la peine:

$L_ {s} = 4 \ cdot \ pi \ cdot r_ {s} ^ {2} \ cdot \ sigma \ cdot T {{{mathrm {eff}}}} {4} \,$ .

Un résultat analogue est obtenu au lieu de faire le calcul pour la surface solaire, en le faisant à distance de la Terre et en utilisant la constante solaire. Le flux émis par le soleil diminue avec la distance car il est réparti sur une plus grande surface. La surface sphérique à la distance de la Terre vaut la peine:

$S = 4 \ cdot \ pi \ cdot a_ {0} ^ {2} = 2.81 \ times 10 ^ {{23}} m ^ {2} \,$ .
La luminosité solaire vaut donc:

$L_ {s} = k \ cdot S = 3,65 x 10 ^ {26} W = 3,65 x 10 ^ {23} kW$
Un résultat analogue est obtenu en effectuant le calcul suivant le raisonnement suivant:

Le diamètre angulaire de la Terre vu du Soleil est d’environ 1/11 700 radians, de sorte que l’angle solide de la Terre par rapport au Soleil est de 1/175 000 000 stéradians. Cela implique que la Terre n’intercepte qu’une partie des 2000 millions de rayonnements émis par le Soleil (environ 3,6 × 10 ²⁶W).

La constante solaire inclut tous les types de rayonnement, pas seulement le visible. La constante solaire est liée à la magnitude apparente du Soleil (l’intensité de sa luminosité reçue par le spectateur) dont la valeur est de -26,8; puisque les deux paramètres décrivent la luminosité observable du Soleil, bien que la magnitude ne concerne que le spectre visible.

Mesures historiques
En 1838, Claude Pouillet fit la première estimation de la constante solaire. À l’aide d’un pyrhéliomètre très simple qu’il a développé, il a obtenu une valeur de 1,228 kW / m², proche de l’estimation actuelle.

En 1875, Jules Violle reprend le travail de Pouillet et propose une estimation un peu plus grande de 1,7 kW / m² basée, en partie, sur une mesure qu’il réalise à partir du Mont-Blanc en France.

En 1884, Samuel Pierpont Langley a tenté d’estimer la constante solaire à partir du mont Whitney en Californie. En prenant des mesures à différents moments de la journée, il a essayé de corriger les effets dus à l’absorption atmosphérique. Cependant, la valeur finale proposée de 2,903 kW / m² était beaucoup trop importante.

Entre 1902 et 1957, des mesures effectuées par Charles Greeley Abbot et d’autres sites à haute altitude ont montré des valeurs comprises entre 1,322 et 1,465 kW / m². Abbot a montré qu’une des corrections de Langley avait été appliquée par erreur. Les résultats d’Abbé variaient entre 1,89 et 2,22 calories (1,318 à 1,548 kW / m²), une variation qui semblait être due au soleil et non à l’atmosphère terrestre.

En 1954, la constante solaire a été évaluée à 2,00 cal / min / cm 2 ± 2%. Les résultats actuels sont inférieurs d’environ 2,5%.

Relation avec d’autres mesures

Irradiation solaire
L’irradiation solaire directe au sommet de l’atmosphère fluctue d’environ 6,9% au cours d’une année (passant de 1,412 kW / m² début janvier à 1,321 kW / m² début juillet) en raison de la distance de la Terre par rapport au Soleil et généralement de beaucoup moins de 0,1% au jour le jour. Ainsi, pour l’ensemble de la Terre (qui a une section transversale de 127 400 000 km²), la puissance est de 1,730 × 1017 W (ou 173 000 térawatts), plus ou moins 3,5% (la moitié de l’aire de répartition annuelle d’environ 6,9%). La constante solaire ne reste pas constante pendant de longues périodes (voir Variation solaire), mais sur une année, la constante solaire varie beaucoup moins que l’irradiance solaire mesurée au sommet de l’atmosphère. Cela est dû au fait que la constante solaire est évaluée à une distance fixe de 1 unité astronomique (UA) alors que l’irradiation solaire sera affectée par l’excentricité de l’orbite terrestre. Sa distance au Soleil varie chaque année entre 147,1 et 106 km à l’aphélie et 152,1 à 106 km au périhélie.

La Terre reçoit une quantité totale de rayonnement déterminée par sa section (π • RE²), mais en tournant, cette énergie est répartie sur toute la surface (4 • π • RE²). Ainsi, le rayonnement solaire entrant moyen, compte tenu de l’angle sous lequel les rayons frappent et que la moitié de la planète ne reçoit aucun rayonnement solaire à tout moment, représente le quart de la constante solaire (environ 340 W / m²). La quantité atteignant la surface de la Terre (en tant qu’insolation) est encore réduite par l’atténuation atmosphérique, qui varie. À tout moment, la quantité de rayonnement solaire reçue à un endroit de la surface de la Terre dépend de l’état de l’atmosphère, de la latitude du lieu et de l’heure de la journée.

Ampleur apparente
La constante solaire comprend toutes les longueurs d’onde du rayonnement électromagnétique solaire, pas seulement la lumière visible (voir Spectre électromagnétique). Il est positivement corrélé avec la magnitude apparente du Soleil qui est −26.8. La constante solaire et la magnitude du soleil sont deux méthodes permettant de décrire la luminosité apparente du soleil, bien que la magnitude ne soit basée que sur la sortie visuelle du soleil.

Le rayonnement total du soleil
Le diamètre angulaire de la Terre vu du Soleil est d’environ 1/11 700 radians (environ 18 secondes d’arc), ce qui signifie que l’angle solide de la Terre vu du Soleil est d’environ 1/175 000 000 d’un stéradian. Ainsi, le Soleil émet environ 2,2 milliards de fois la quantité de rayonnement captée par la Terre, soit environ 3,86 × 1026 watts.

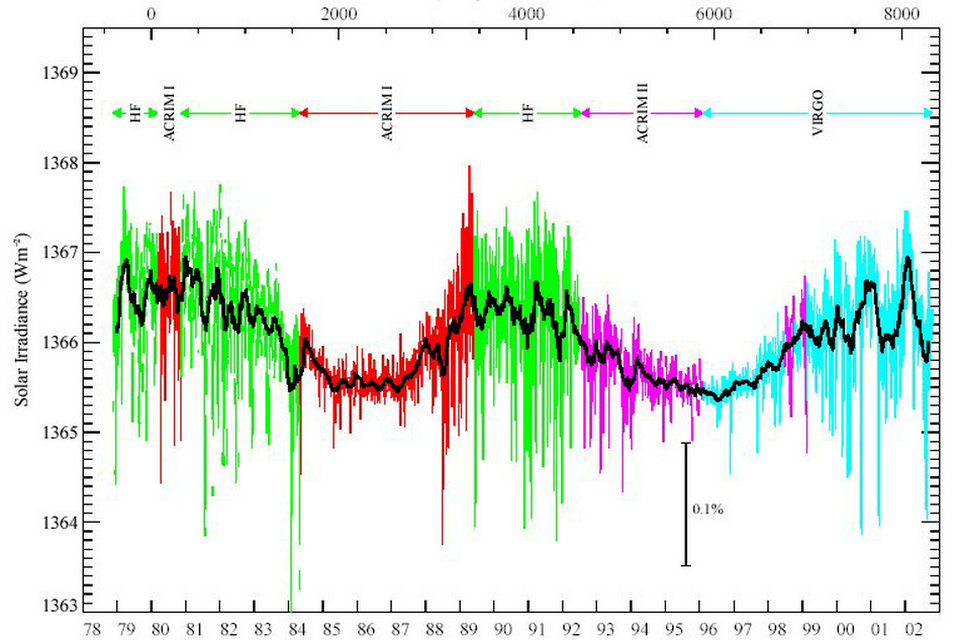
Les variations passées de l’irradiance solaire
Les observations spatiales de l’irradiance solaire ont commencé en 1978. Ces mesures montrent que la constante solaire n’est pas constante. Il varie avec le cycle solaire des taches solaires de 11 ans. En remontant dans le temps, il faut s’appuyer sur des reconstructions d’irradiance, en utilisant des taches solaires depuis 400 ans ou des radionucléides cosmogéniques depuis 10 000 ans. De telles reconstructions montrent que l’irradiance solaire varie avec des périodicités distinctes. Ces cycles sont: 11 ans (Schwabe), 88 ans (cycle de Gleisberg), 208 ans (cycle de DeVries) et 1 000 ans (cycle de Foucault).

Sur des milliards d’années, le Soleil se dilate progressivement et émet plus d’énergie à partir de la plus grande surface résultante. La question irrésolue de savoir comment expliquer l’évidence géologique de l’eau liquide sur la Terre il y a des milliards d’années, alors que la luminosité du soleil ne représentait que 70% de sa valeur actuelle, est connue sous le nom de faible paradoxe solaire.

Variations dues aux conditions atmosphériques
Au maximum, environ 75% de l’énergie solaire atteint la surface de la Terre, car même avec un ciel sans nuages, elle est partiellement réfléchie et absorbée par l’atmosphère. Même les légers cirrus réduisent ce pourcentage à 50% et les cirrus, à 40%. Ainsi, l’énergie solaire arrivant à la surface peut varier de 550 W / m² avec des cirrus à 1025 W / m² avec un ciel dégagé.

Variation
Le rayonnement émis par le Soleil n’est pas exactement constant, mais souffre de fluctuations chaotiques de très faible amplitude et d’oscillations périodiques décrites comme des cycles d’activité, ainsi que de variations tendancielles par lesquelles la luminosité du Soleil a lentement augmenté au fil du temps.

Les variations périodiques semblent consister en plusieurs oscillations de différentes périodes (durée), la plus connue étant celle de 11 ans qui se manifeste par un cycle de variation de l’abondance des taches solaires dans la photosphère. Les cycles récents montrent une variation de la luminosité solaire dans les limites de 0,1%; Cependant, à partir du minimum de Maunder, une période sans taches entre 1650 et 1700, le rayonnement solaire aurait pu augmenter de 0,6%.

Les modèles théoriques du développement du Soleil impliquent qu’il y a environ 3 milliards d’années, lorsque le système solaire était âgé d’un tiers seulement, le Soleil n’émettait que 75% de l’énergie qu’il émet actuellement. Le climat de la Terre était moins froid que ne l’indiquent ces données, car la composition de l’atmosphère était très différente, beaucoup plus abondante dans les gaz à effet de serre, notamment le dioxyde de carbone (CO ₂ ) et l’ammoniac (NH ₃ ).

D’autres variations de nature cyclique ont à voir avec les paramètres orbitaux de la Terre, en particulier avec l’excentricité. Cela n’affecte pas l’énergie moyenne reçue à long terme, mais affecte les variations saisonnières. Actuellement, la Terre se trouve dans son périhélie au début du mois de janvier, coïncidant presque avec le solstice d’hiver, ce qui contribue à ce que l’hémisphère nord collecte plus d’énergie solaire que le Sud. Mais la date du périhélie (et de l’aphélie) oscille avec une très longue période.
En tout état de cause, l’excentricité de l’orbite terrestre est relativement faible, mais elle est cependant importante dans d’autres planètes, telles que Mars et surtout Pluton (maintenant considérée comme « planète naine »). Dans ceux-ci, la différence d’énergie interceptée à différents moments de l’année peut être considérable. Le tableau suivant présente les constantes solaires des planètes du système solaire, calculées en fonction de leur distance moyenne.

Pertinence
La valeur de la constante solaire, ainsi que sa stabilité relative, sont fondamentales pour la plupart des processus terrestres les plus importants. En particulier, pour la détermination du climat, des processus géologiques externes et pour la vie. Aussi pour l’avenir de l’humanité, du moins comme cela dépend du développement technologique des énergies renouvelables.

Constante solaire pour les différentes planètes
Le flux émis par le soleil diminue avec la distance car il est réparti sur une plus grande surface.Supposons que nous appelions ${$ $K_ {0} \,$ à la constante solaire à la distance de la Terre (1 unité astronomique) et K à la distance r exprimée en UA de toute planète solaire, il sera vrai que la luminosité solaire ne change pas, c’est-à-dire:
$L_ {s} = K_ {0} \ cdot 4 \ cdot \ pi \ cdot 1 ^ {2} = K \ cdot 4 \ cdot \ pi \ cdot r ^ {2} \,$
c’est-à-dire:

$K = {\ frac {K_ {0}} {r ^ {2}}} \$

Supposons par exemple que la planète Mars qui est à 1,5236 UA de la constante solaire vaut la peine:

$K = {\ frac {1366} {1,5236 ^ {2}} = 588,45 {\ frac {W} {m ^ {2}}},$

Température effective sur différentes planètes
Pour calculer la température effective dans les différentes planètes, le calcul du bilan radiatif terrestre doit être effectué mais généralisé pour les planètes. On suppose que chaque planète a atteint l’équilibre en interceptant du Soleil la même énergie qui rayonne de sa température.

$Energie {{intercepté}} = K \ cdot \ pi \ cdot r ^ {2} \,$ où r est le rayon de la planète.

$Energie _ {absorbé}} = K \ cdot \ pi \ cdot r ^ {2} \ cdot (1-a) \,$ C’est à l’albédo

$Energie {irradiée}} = 4 \ cdot \ pi \ cdot r ^ {2} \ sigma \ cdot T_ {e} ^ {4} \,$

La raison de 4 est que seule la section de la planète coupe l’énergie solaire alors que toute la surface de la planète la rayonne.

Comme l’énergie absorbée et rayonnée est égale à l’équilibre thermique, il en résulte:

$T_ {e} = {\ sqrt [{4}] {{\ frac {K \ cdot (1-a)} {4 \ cdot \ sigma}}}}$

L’évaluation de la formule donne les différentes températures efficaces des planètes. Ces températures ne doivent pas être confondues avec les températures de surface, car l’atmosphère et les nuages reflètent une partie du rayonnement solaire à ondes courtes tandis que les ondes longues émises par le rayonnement thermique de la planète sont partiellement absorbées par les gaz à effet de serre. cas de Vénus alors que si l’atmosphère est mince comme dans le cas de Mars, il ne devrait pas y avoir beaucoup de différence.

Constantes solaires ( K ) des planètes du système solaire et températures effectives (**T _e** )
Planète	K (W / m²)	K / K ₀	Albedo	T _e (K)
Mercure	9040	6,7	0,058	442
Vénus	2610	1,9	0,71	244
Terre	1360	1	0,33	253
Mars	590	0,4	0,17	216
Jupiter	cinquante	0,04	0,52	87
Saturne	quinze	0,01	0,47	63
Uranus	3.7	0,003	0,51	33
Neptune	1,5	0,001	0,41	32