Constante solar – HiSoUR Arte Cultura Historia

La constante solar es una densidad de flujo que mide la radiación solar media electromagnética (irradiancia solar) por unidad de área. Se mide en una superficie perpendicular a los rayos, una unidad astronómica (AU) desde el Sol (aproximadamente la distancia desde el Sol hasta la Tierra).

La constante solar incluye todos los tipos de radiación solar, no solo la luz visible. Se mide por satélite como 1.361 kilovatios por metro cuadrado (kW / m²) al mínimo solar y aproximadamente 0.1% mayor (aproximadamente 1.362 kW / m²) al máximo solar.

La «constante» solar no es una constante física en el sentido científico CODATA moderno; es decir, no es como la constante de Planck o la velocidad de la luz que son absolutamente constantes en física. La constante solar es un promedio de un valor variable. En los últimos 400 años, ha variado menos de 0.2 por ciento.

Fórmula
Para calcular la constante solar, es suficiente dividir el flujo de energía que emite el Sol por la proporción de áreas entre la superficie del Sol. $r_ {s} \,$ (la radio solar) y la de una esfera de radio $a_ {0} \,$ (una unidad astronómica) de eso. Para obtener este valor, que en la práctica se mide con satélites, se debe utilizar como una temperatura efectiva $T {{{mathrm {eff}}}}$ ) Del Sol 5776 el valor K.
${\ displaystyle K = \ sigma \ cdot T _ {\ mathrm {eff}} ^ {4} \ cdot ({\ frac {r_ {s}} {a_ {0}}}) ^ {2} = 1366 \ W \ cdot {m ^ {- 2}}}$
La constante solar se puede expresar en ${\ frac {calorias} {cm ^ {2} \ cdot minute}} \,$ . Para hacer esto, recuerda 1 de julio = 0.24 calorías, 1 minuto = 60 s y 1 m ² = 10 ⁴ cm ²
$K = 1366 {\ frac {joules} {s \ cdot m ^ {2}} = {\ frac {1366 \ cdot 0.24 \ cdot 60} {10 ^ {4}}} = 1,967 {\ frac {calories}} { cm ^ {2} \ cdot minute}} \ approx 2 {\ frac {calorias} {cm ^ {2} \ cdot minute}} \,$ .
Una unidad muy utilizada para medir la energía que llega a la parte superior de la atmósfera en un día es:
$1langley = 1 {\ frac {caloria} {cm ^ {2}}} \,$

Por lo tanto, un lugar en la latitud 30 ° N recibe el 21 de junio, el día del solsticio de verano una insolación de 1004,7 langleys / día y el 21 de diciembre, el día del solsticio de invierno solo 480,4 langleys / día.

Por otro lado, se puede calcular la insolación anual en la parte superior de la atmósfera en diferentes latitudes. Para el polo, la insolación anual es de 133,2 kilolangleys / año, mientras que en el ecuador se eleva a 320,9 kilolangleys / año, donde el klangley = 1000 langleys.

Cálculo
La irradiación solar se mide por satélite sobre la atmósfera terrestre, y luego se ajusta usando la ley del cuadrado inverso para inferir la magnitud de la radiación solar en una Unidad Astronómica (UA) para evaluar la constante solar. El valor promedio aproximado citado, 1.3608 ± 0.0005 kW / m², que es de 81.65 kJ / m² por minuto, es equivalente a aproximadamente 1.951 calorías por minuto por centímetro cuadrado, o 1.951 langleys por minuto.

La salida solar es casi constante, pero no del todo. Las variaciones en la irradiación solar total (TSI) fueron pequeñas y difíciles de detectar con precisión con la tecnología disponible antes de la era del satélite (± 2% en 1954). La producción solar total ahora se mide como variable (en los últimos tres ciclos de manchas solares de 11 años) en aproximadamente 0.1%; ver la variación solar para más detalles.

Luminosidad solar
la energía se llama energía emitida por el Sol en la unidad de tiempo. Por lo tanto, vale la pena:

$L_ {s} = 4 \ cdot \ pi \ cdot r_ {s} ^ {2} \ cdot \ sigma \ cdot T {{{mathrm {eff}}}} ^ {4} \,$ .

Se obtiene un resultado análogo en lugar de hacer el cálculo para la superficie solar, hacerlo a una distancia de la Tierra y usar la constante solar. El flujo emitido por el Sol disminuye con la distancia porque se distribuye en una superficie más grande. La superficie esférica a la distancia en la que se encuentra la Tierra vale:

$S = 4 \ cdot \ pi \ cdot a_ {0} ^ {2} = 2.81 \ times 10 ^ {{23}} m ^ {2} \,$ .
La luminosidad solar por lo tanto vale la pena:

$L_ {s} = k \ cdot S = 3,65 x 10 ^ {26} W = 3,65 x 10 ^ {23} kW$
El resultado análogo se obtiene haciendo el cálculo por el siguiente razonamiento:

El diámetro angular de la Tierra visto desde el Sol es aproximadamente 1 / 11.700 radianes, por lo que el ángulo sólido de la Tierra con respecto al Sol es de 1 / 175,000,000 estereorradianes. Esto implica que la Tierra intercepta solo una parte de los 2000 millones de radiación que emite el Sol (aproximadamente 3.6 × 10 ²⁶ W).

La constante solar incluye todos los tipos de radiación, no solo la visible. La constante solar se relaciona con la magnitud aparente del Sol (la intensidad de su brillo según lo recibe el espectador) cuyo valor es -26.8; ya que ambos parámetros vienen a describir el brillo observable del Sol, aunque la magnitud se refiere solo al espectro visible.

Mediciones históricas
En 1838, Claude Pouillet hizo la primera estimación de la constante solar. Usando un pirheliómetro muy simple que desarrolló, obtuvo un valor de 1.228 kW / m², cerca de la estimación actual.

En 1875, Jules Violle reanudó el trabajo de Pouillet y ofreció una estimación algo mayor de 1.7 kW / m² basada, en parte, en una medición que hizo desde el Mont Blanc en Francia.

En 1884, Samuel Pierpont Langley intentó estimar la constante solar de Mount Whitney en California. Al tomar lecturas en diferentes momentos del día, trató de corregir los efectos debidos a la absorción atmosférica. Sin embargo, el valor final que él propuso, 2.903 kW / m², era demasiado grande.

Entre 1902 y 1957, las mediciones de Charles Greeley Abbot y otros en varios sitios de gran altitud encontraron valores entre 1.322 y 1.465 kW / m². Abbot mostró que una de las correcciones de Langley se aplicó erróneamente. Los resultados de Abbot variaron entre 1,89 y 2,22 calorías (1,318 a 1,548 kW / m²), una variación que parecía deberse al Sol y no a la atmósfera de la Tierra.

En 1954 la constante solar se evaluó como 2.00 cal / min / sq cm ± 2%. Los resultados actuales son aproximadamente 2.5 por ciento más bajos.

Relación con otras medidas

Radiacion solar
La irradiación solar directa real en la parte superior de la atmósfera fluctúa alrededor de 6.9% durante un año (de 1.412 kW / m² a principios de enero a 1.321 kW / m² a principios de julio) debido a la distancia variable de la Tierra del Sol, y típicamente por mucho menos del 0.1% de día a día.Por lo tanto, para toda la Tierra (que tiene una sección transversal de 127,400,000 km²), la potencia es de 1.730 × 1017 W (o 173,000 teravatios), más o menos 3.5% (la mitad del rango anual de aproximadamente 6.9%). La constante solar no permanece constante durante largos períodos de tiempo (ver variación solar), pero durante un año la constante solar varía mucho menos que la irradiancia solar medida en la parte superior de la atmósfera. Esto se debe a que la constante solar se evalúa a una distancia fija de 1 Unidad Astronómica (UA) mientras que la irradiancia solar se verá afectada por la excentricidad de la órbita de la Tierra. Su distancia al Sol varía anualmente entre 147.1 • 106 km en el afelio y 152.1 • 106 km en el perihelio.

La Tierra recibe una cantidad total de radiación determinada por su sección transversal (π • RE²), pero a medida que gira esta energía se distribuye por toda el área superficial (4 • π • RE²). Por lo tanto, la radiación solar entrante promedio, teniendo en cuenta el ángulo al que golpean los rayos y que en cualquier momento la mitad del planeta no recibe ninguna radiación solar, es un cuarto de la constante solar (aproximadamente 340 W / m²). La cantidad que alcanza la superficie de la Tierra (como insolación) se reduce aún más por la atenuación atmosférica, que varía. En un momento dado, la cantidad de radiación solar recibida en una ubicación en la superficie de la Tierra depende del estado de la atmósfera, la latitud de la ubicación y la hora del día.

Magnitud aparente
La constante solar incluye todas las longitudes de onda de la radiación electromagnética solar, no solo la luz visible (ver Espectro electromagnético). Está positivamente correlacionado con la magnitud aparente del Sol que es -26.8. La constante solar y la magnitud del Sol son dos métodos para describir el brillo aparente del Sol, aunque la magnitud se basa solo en la salida visual del Sol.

La radiación total del sol
El diámetro angular de la Tierra visto desde el Sol es de aproximadamente 1 / 11.700 radianes (alrededor de 18 segundos de arco), lo que significa que el ángulo sólido de la Tierra visto desde el Sol es aproximadamente 1 / 175,000,000 de un estereorradián. Por lo tanto, el Sol emite aproximadamente 2,2 mil millones de veces la cantidad de radiación que captura la Tierra, en otras palabras, alrededor de 3,86 × 1026 vatios.

Variaciones pasadas en la irradiancia solar
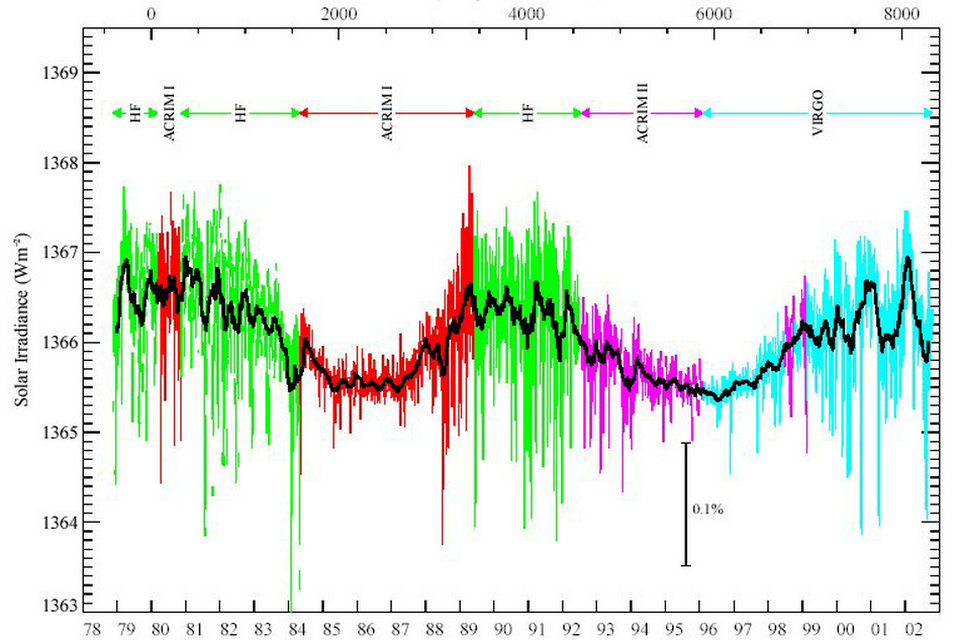
Las observaciones espaciales de la irradiancia solar comenzaron en 1978. Estas mediciones muestran que la constante solar no es constante. Varía con el ciclo solar de manchas solares de 11 años. Al retroceder en el tiempo, uno debe confiar en las reconstrucciones de irradiación, usando manchas solares durante los últimos 400 años o radionucleidos cosmógenos en 10.000 años. Tales reconstrucciones muestran que la irradiancia solar varía con distintas periodicidades. Estos ciclos son: 11 años (Schwabe), 88 años (ciclo Gleisberg), 208 años (ciclo DeVries) y 1.000 años (ciclo Eddy).

Durante miles de millones de años, el Sol se está expandiendo gradualmente y emitiendo más energía del área de superficie más grande resultante. La cuestión no resuelta de cómo explicar la clara evidencia geológica de agua líquida en la Tierra hace miles de millones de años, en un momento en que la luminosidad del sol era solo el 70% de su valor actual, se conoce como la débil paradoja del Sol joven.

Variaciones debidas a las condiciones atmosféricas
Como máximo, cerca del 75% de la energía solar realmente llega a la superficie de la tierra, ya que incluso con un cielo sin nubes, la atmósfera la refleja y absorbe parcialmente. Incluso las nubes cirrus ligeras reducen esto al 50%, las nubes cirrus más fuertes al 40%. Por lo tanto, la energía solar que llega a la superficie puede variar de 550 W / m² con cirros a 1025 W / m² con cielo despejado.

Variación
La radiación emitida por el Sol no es exactamente constante, pero sufre fluctuaciones caóticas de amplitud muy pequeña y oscilaciones periódicas descritas como ciclos de actividad, así como variaciones de tendencia por las cuales el brillo del Sol ha crecido lentamente a lo largo del tiempo de su historia.

Las variaciones periódicas parecen consistir en varias oscilaciones de diferente período (duración), de las cuales la más conocida es la de 11 años que se manifiesta como un ciclo de variación de la abundancia de manchas solares en la fotosfera. Los ciclos recientes muestran una variación del brillo solar dentro de los límites del 0.1%; Sin embargo, desde el mínimo de Maunder, un tiempo sin manchas entre 1650 y 1700, la radiación solar podría haber crecido hasta en un 0,6%.

Los modelos teóricos del desarrollo del Sol implican que hace unos 3.000 millones de años, cuando el Sistema Solar tenía solo un tercio de su edad, el Sol emitía solo el 75% de la energía que emite actualmente. El clima de la Tierra era menos frío de lo que implican estos datos, porque la composición de la atmósfera era muy diferente, mucho más abundante en los gases de efecto invernadero, especialmente el dióxido de carbono (CO ₂ ) y el amoníaco (NH ₃ ).

Otras variaciones de naturaleza cíclica tienen que ver con los parámetros orbitales de la Tierra, especialmente con la excentricidad. Esto no afecta la energía promedio recibida a largo plazo, pero sí afecta las variaciones estacionales. Actualmente, la Tierra está en su perihelio a principios de enero, casi coincidiendo con el solsticio de invierno, lo que contribuye a que el hemisferio norte recolecte más energía solar que el sur. Pero la fecha del perihelio (y del afelio) oscila con un período muy largo.
En cualquier caso, la excentricidad de la órbita de la Tierra es relativamente pequeña, pero es grande, sin embargo, en otros planetas, como Marte y, sobre todo, Plutón (ahora considerado «planeta enano»). En estos, la diferencia de energía interceptada en diferentes momentos del año puede ser considerable. La siguiente tabla presenta las constantes solares de los planetas del Sistema Solar, calculadas de acuerdo con su distancia promedio.

Pertinencia
El valor de la constante solar, así como su estabilidad relativa, son fundamentales para muchos de los procesos terrestres más importantes. En particular, para la determinación del clima, procesos geológicos externos y para la vida. También para el futuro de la humanidad, al menos ya que depende del desarrollo tecnológico de la energía renovable.

Constante solar para los diferentes planetas
El flujo emitido por el Sol disminuye con la distancia porque se distribuye en una superficie más grande. Supongamos que llamamos ${$ $K_ {0} \,$ a la constante solar a la distancia de la Tierra (1 unidad astronómica) y K a la distancia r expresada en UA de cualquier planeta solar, será cierto que la luminosidad solar no cambia, es decir:
$L_ {s} = K_ {0} \ cdot 4 \ cdot \ pi \ cdot 1 ^ {2} = K \ cdot 4 \ cdot \ pi \ cdot r ^ {2} \,$
es decir:

$K = {\ frac {K_ {0}} {r ^ {2}}} \,$

Supongamos, por ejemplo, que el planeta Marte que está a 1.5236 UA de la constante solar valdrá:

$K = {\ frac {1366} {1,5236 ^ {2}} = 588.45 {\ frac {W} {m ^ {2}}} \,$

Temperatura efectiva en diferentes planetas
Para calcular la temperatura efectiva en los diferentes planetas, el cálculo del balance radiativo terrestre debe ser generalizado para los planetas. Se supone que cada planeta ha alcanzado el equilibrio al interceptar del Sol la misma energía que irradia desde su temperatura.

$Energía {{interceptada}} = K \ cdot \ pi \ cdot r ^ {2} \,$ donde r es el radio del planeta.

$Energía _ {absorbida}} = K \ cdot \ pi \ cdot r ^ {2} \ cdot (1-a) \,$ Es al albedo

$Energía {{irradiated}} = 4 \ cdot \ pi \ cdot r ^ {2} \ sigma \ cdot T_ {e} ^ {4} \,$

La razón para 4 es que solo la sección del planeta se cruza con la energía solar mientras que toda la superficie del planeta la irradia.

Como la energía absorbida e irradiada es igual al equilibrio térmico, resulta:

$T_ {e} = {\ sqrt [{4}] {{\ frac {K \ cdot (1-a)} {4 \ cdot \ sigma}}}} \,$

La evaluación de la fórmula proporciona las diferentes temperaturas efectivas de los planetas. Estas temperaturas no deben confundirse con las temperaturas superficiales, ya que la atmósfera y las nubes reflejan parte de la radiación solar de onda corta, mientras que las ondas largas emitidas por la radiación térmica del planeta son absorbidas en parte por gases de efecto invernadero, lo que aumenta significativamente la temperatura superficial. caso de Venus, si la atmósfera es delgada como en el caso de Marte, no debería haber mucha diferencia.

Constantes solares ( K ) de los planetas del Sistema Solar y temperaturas efectivas ( **T _e**)
Planeta	K (W / m²)	K / K ₀	Albedo	T _e (K)
Mercurio	9040	6.7	0.058	442
Venus	2610	1.9	0.71	244
Tierra	1360	1	0.33	253
Marte	590	0.4	0.17	216
Júpiter	cincuenta	0.04	0,52	87
Saturno	quince	0.01	0.47	63
Urano	3.7	0.003	0,51	33
Neptuno	1,5	0.001	0.41	32