Der Begriff Space-Syntax umfasst eine Reihe von Theorien und Techniken zur Analyse räumlicher Konfigurationen. Es wurde von Bill Hillier, Julienne Hanson und Kollegen am Bartlett, University College London in den späten 1970er Jahren bis Anfang der 1980er Jahre als ein Werkzeug konzipiert, um Stadtplanern zu helfen, die wahrscheinlichen sozialen Effekte ihrer Entwürfe zu simulieren.

These
Die allgemeine Idee ist, dass Räume in Komponenten zerlegt, als Netzwerke von Auswahlmöglichkeiten analysiert und dann als Karten und Graphen dargestellt werden können, die die relative Konnektivität und Integration dieser Räume beschreiben. Es beruht auf drei Grundkonzeptionen des Raumes:

ein Isovist (popularisiert von Michael Benedikt an der Universität von Texas) oder ein Sicht- oder Sichtpolygon, das Sichtfeld von einem bestimmten Punkt aus
axialer Raum (Idee von Bill Hillier an der UCL), eine gerade Sichtlinie und ein möglicher Weg
konvexer Raum (popularisiert von John Peponis und seinen Mitarbeitern bei Georgia Tech), eine besetzbare Leere, in der, wenn man sich als Drahtmodelldiagramm vorstellt, keine Linie zwischen zwei Punkten außerhalb ihres Umfangs verläuft: Alle Punkte innerhalb des Polygons sind für alle anderen sichtbar Punkte innerhalb des Polygons.
Die drei beliebtesten Wege zur Analyse eines Straßennetzes sind Integration, Auswahl und Tiefenabstand.

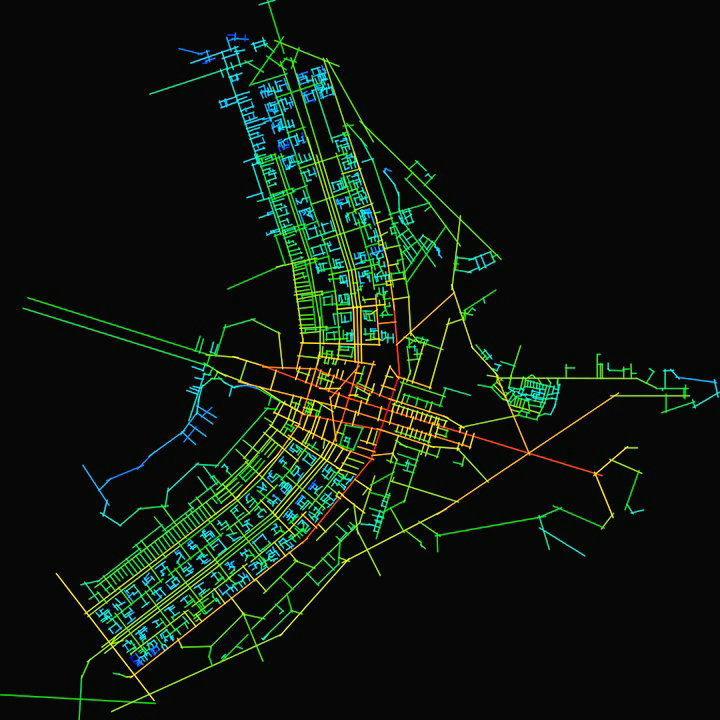
Integration misst, wie viele Abbiegungen von einem Straßensegment gemacht werden müssen, um alle anderen Straßensegmente im Netzwerk auf kürzesten Wegen zu erreichen. Wenn die Anzahl von Windungen analysiert wird, die erforderlich ist, um alle Segmente in dem Graphen zu erreichen, wird gesagt, dass die Analyse die Integration bei dem Radius ’n‘ misst. Das erste überschneidende Segment benötigt nur eine Umdrehung, die zweiten zwei Umdrehungen und so weiter. Die Straßensegmente, die die wenigsten Kurven benötigen, um alle anderen Straßen zu erreichen, werden als „am besten integriert“ bezeichnet und werden normalerweise mit heißeren Farben wie rot oder gelb dargestellt. Die Integration kann auch auf lokaler Ebene statt auf der Ebene des gesamten Netzwerks analysiert werden. Im Fall von Radius 4 beispielsweise werden nur vier Windungen gezählt, die von jedem Straßensegment ausgehen.
Theoretisch zeigt das Integrationsmaß die kognitive Komplexität des Erreichens einer Straße und wird oft argumentiert, um die Fußgängerbenutzung einer Straße „vorherzusagen“: Je einfacher es ist, eine Straße zu erreichen, desto beliebter sollte es sein. Es gibt zwar Hinweise darauf, dass dies zutrifft, aber die Methode ist auf lange, gerade Straßen ausgerichtet, die sich mit vielen anderen Straßen kreuzen. Solche Straßen, wie die Oxford Street in London, sind besonders stark integriert. Eine leicht kurvige Straße gleicher Länge würde jedoch typischerweise in einzelne gerade Segmente unterteilt, die nicht als eine einzige Linie gezählt werden, wodurch kurvige Straßen weniger integriert in die Analyse erscheinen.

Die Choice-Maßnahme ist am einfachsten als „Wasserfluss“ im Straßennetz zu verstehen. Stellen Sie sich vor, dass jedes Straßensegment eine Anfangsladung von einer Wassereinheit erhält, die dann vom Start-Straßensegment zu allen Segmenten beginnt, die sukzessive damit verbunden sind. Jedes Mal, wenn eine Kreuzung angezeigt wird, wird der verbleibende Wert des Flusses gleichmäßig auf die sich aufteilenden Straßen aufgeteilt, bis alle anderen Straßensegmente in der Grafik erreicht sind. Zum Beispiel wird an der ersten Kreuzung mit einer einzelnen anderen Straße der Anfangswert von eins in zwei verbleibende Werte von einer Hälfte geteilt und den zwei sich schneidenden Straßensegmenten zugeordnet. Wenn Sie weiter nach unten gehen, wird der verbleibende halbe Wert erneut zwischen den sich kreuzenden Straßen aufgeteilt und so weiter. Wenn dieselbe Prozedur unter Verwendung jedes Segments als Startpunkt für den Anfangswert von Eins durchgeführt wurde, erscheint ein Diagramm der Endwerte. Die Straßen mit den höchsten Gesamtwerten des akkumulierten Flusses sollen die höchsten Auswahlwerte haben.
Wie bei der Integration kann die Auswahlanalyse auf begrenzte lokale Radien beschränkt werden, z. B. 400 m, 800 m, 1600 m. Die Interpretation von Choice-Analysen ist komplizierter als die Integration. Die Space-Syntax argumentiert, dass diese Werte oft den Straßenfluss des Autoverkehrs vorhersagen, aber genau genommen kann die Choice-Analyse auch die Anzahl der Kreuzungen darstellen, die überquert werden müssen, um eine Straße zu erreichen. Da jedoch die Strömungswerte an jeder Kreuzung geteilt (nicht subtrahiert) werden, zeigt die Ausgabe eine exponentielle Verteilung. Es wird als am besten angesehen, ein Protokoll der Basis zwei der endgültigen Werte zu nehmen, um ein genaueres Bild zu erhalten.

Die Tiefenentfernung ist die intuitivste der Analysemethoden. Es erklärt den linearen Abstand vom Mittelpunkt jedes Straßensegments zu den Mittelpunkten aller anderen Segmente. Wenn jedes Segment nacheinander als Startpunkt gewählt wird, wird ein Graph kumulativer Endwerte erhalten. Die Straßen mit den niedrigsten Tiefenabstand-Werten sollen allen anderen Straßen am nächsten liegen. Auch hier kann der Suchradius auf eine beliebige Entfernung beschränkt werden.
Anwendungen
Von diesen Komponenten wird angenommen, dass es möglich ist, zu quantifizieren und zu beschreiben, wie einfach jeder Raum navigierbar ist, was nützlich für die Gestaltung von Museen, Flughäfen, Krankenhäusern und anderen Umgebungen ist, in denen die Wegfindung ein signifikantes Problem ist. Space-Syntax wurde auch angewendet, um die Korrelation zwischen räumlichen Layouts und sozialen Auswirkungen wie Kriminalität, Verkehrsfluss und Flächenumsatz vorherzusagen.

Geschichte
Die Raumsyntax hat sich zu einem Werkzeug entwickelt, das weltweit in einer Vielzahl von Forschungsbereichen und Designanwendungen in Architektur, Städtebau, Planung, Verkehr und Innenarchitektur verwendet wird. Im Allgemeinen verwendet die Analyse eines von vielen Softwareprogrammen, mit denen Forscher Graphen von einer (oder mehreren) der primären räumlichen Komponenten analysieren können.

In den letzten zehn Jahren wurden Techniken der Weltraumsyntax für die Archäologie, Informationstechnologie, Stadt- und Humangeographie und Anthropologie eingesetzt. Seit 1997 hat die Space-Syntax-Gemeinschaft alle zwei Jahre Konferenzen abgehalten, und viele Zeitschriftenartikel wurden zu diesem Thema veröffentlicht, hauptsächlich in Umwelt und Planung B.

Kritik
Die mathematische Zuverlässigkeit der Weltraumsyntax wurde in letzter Zeit aufgrund einer Reihe von Paradoxien, die unter bestimmten geometrischen Konfigurationen auftreten, kritisch untersucht. Diese Paradoxien wurden von Carlo Ratti am Massachusetts Institute of Technology hervorgehoben, aber in einem leidenschaftlichen akademischen Austausch mit Bill Hillier und Alan Penn [2004] bestritten. Es gab Versuche, die Raum-Syntax mit traditionelleren Transport-Engineering-Modellen zu kombinieren, Kreuzungen als Knoten zu verwenden und Sichtbarkeitsgraphen zu konstruieren, um sie zu verknüpfen, von Forschern wie Bin Jiang, Valerio Cutini und Michael Batty. Kürzlich gab es auch Forschungsentwicklungen, die die Raumsyntax mit geographischen Zugänglichkeitsanalysen in GIS kombinieren, wie beispielsweise die von der Forschungsgruppe Spatial Analysis and Design am Royal Institute of Technology in Stockholm, Schweden, entwickelten Platz-Syntax-Modelle. Eine Reihe von http://journals.sagepub.com/doi/abs/10.108/b32045 interdisziplinären Arbeiten, die 2006 von Vito Latora, Sergio Porta und Kollegen veröffentlicht wurden und einen Netzwerkansatz für die Analyse und das Design von Straßenzentralität vorschlugen, haben die Space Syntax hervorgehoben. Beitrag zu Jahrzehnten früherer Studien in der Physik räumlicher komplexer Netzwerke.