In colorimetry and color theory, lightness, also known as value or tone, is a representation of variation in the perception of a color or color space’s brightness. It is one of the color appearance parameters of any color appearance model.
Various color models have an explicit term for this property. The Munsell color model uses the term value, while the HSL color model, HCL color space and Lab color space use the term lightness. The HSV model uses the term value a little differently: a color with a low value is nearly black, but one with a high value is the pure, fully saturated color.
In subtractive color (i.e. paints) value changes can be achieved by adding black or white to the color. However, this also reduces saturation. Chiaroscuro and Tenebrism both take advantage of dramatic contrasts of value to heighten drama in art. Artists may also employ shading, subtle manipulation of value.
Relationship to value and relative luminance
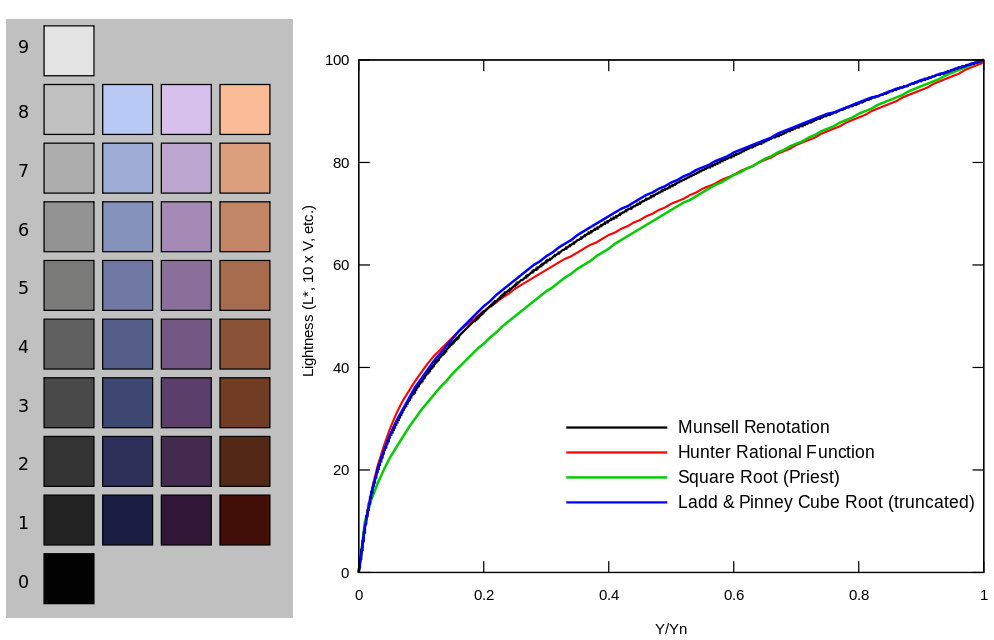
The Munsell value has long been used as a perceptually uniform lightness scale. A question of interest is the relationship between the Munsell value scale and the relative luminance. Aware of the Weber–Fechner law, Munsell remarked “Should we use a logarithmic curve or curve of squares?” Neither option turned out to be quite correct; scientists eventually converged on a roughly cube-root curve, consistent with the Stevens’ power law for brightness perception, reflecting the fact that lightness is proportional to the number of nerve impulses per nerve fiber per unit time. The remainder of this section is a chronology of lightness approximations, leading to CIE LAB.
Note. – Munsell’s V runs from 0 to 10, while Y typically runs from 0 to 100 (often interpreted as a percentage). Typically, the relative luminance is normalized so that the “reference white” (say, magnesium oxide) has a tristimulus value of Y = 100. Since the reflectance of magnesium oxide (MgO) relative to the perfect reflecting diffuser is 97.5%, V = 10 corresponds to Y = 100/97.5% ≈ 102.6 if MgO is used as the reference.
1920
Priest et al. provide a basic estimate of the Munsell value (with Y running from 0 to 1 in this case):
1933
Munsell, Sloan, and Godlove launch a study on the Munsell neutral value scale, considering several proposals relating the relative luminance to the Munsell value, and suggest:
1943
Newhall, Nickerson, and Judd prepare a report for the Optical Society of America. They suggest a quintic parabola (relating the reflectance in terms of the value):
1943
Using Table II of the O.S.A. report, Moon and Spencer express the value in terms of the relative luminance:
1944
Saunderson and Milner introduce a subtractive constant in the previous expression, for a better fit to the Munsell value. Later, Jameson and Hurvich claim that this corrects for simultaneous contrast effects.
1955
Ladd and Pinney of Eastman Kodak are interested in the Munsell value as a perceptually uniform lightness scale for use in television. After considering one logarithmic and five power-law functions (per Stevens’ power law), they relate value to reflectance by raising the reflectance to the power of 0.352:
Realizing this is quite close to the cube root, they simplify it to:
1958
Glasser et al. define the lightness as ten times the Munsell value (so that the lightness ranges from 0 to 100):
1964
Wyszecki simplifies this to:
This formula approximates the Munsell value function for 1% < Y < 98% (it is not applicable for Y < 1%) and is used for the CIE 1964 color space.
1976
CIE LAB uses the following formula:
where Yn is the CIE XYZ Y tristimulus value of the reference white point (the subscript n suggests “normalized”) and is subject to the restriction Y/Yn > 0.01. Pauli removes this restriction by computing a linear extrapolation which maps Y/Yn = 0 to L* = 0 and is tangent to the formula above at the point at which the linear extension takes effect. First, the transition point is determined to be Y/Yn = (6/29)^3 ≈ 0.008,856, then the slope of (29/3)^3 ≈ 903.3 is computed. This gives the two-part function:
The lightness is then:
At first glance, you might approximate the lightness function by a cube root, an approximation that is found in much of the technical literature. However, the linear segment near black is significant, and so the 116 and 16 coefficients. The best-fit pure power function has an exponent of about 0.42, far from 1/3.
An approximately 18% grey card, having an exact reflectance of , has a lightness value of 50. It is called “mid grey” because its lightness is midway between black and white.
Other psychological effects
This subjective perception of luminance in a non-linear fashion is one thing that makes gamma compression of images worthwhile. Beside this phenomenon there are other effects involving perception of lightness. Chromacity can affect perceived lightness as described by the Helmholtz–Kohlrausch effect. Though the CIE LAB space and relatives do not account for this effect on lightness, it may be implied in the Munsell color model. Light levels may also affect perceived chromacity, as with the Purkinje effect.
Source From Wikipedia