キネマティクスは、起源の原因（力）を考慮せずに固体物体の動きを記述し、主に時間の関数における歴史の研究に限定された物理学の枝である。 このために、速度と加速度を使用します。速度と加速度は、時間の関数として位置がどのように変化するかを表します。 速度は、変位と使用された時間との間の商として決定され、加速度は、速度の変化と使用される時間との間の商である。

キネマティクスの基本要素
キネマティクスの基本要素は、空間、時間、モバイルです。

古典力学では、絶対空間の存在が認められる。すなわち、すべての物質的対象の前の空間であり、これらの存在とは無関係である。 この空間はすべての物理現象が起こる段階であり、物理学のすべての法則が物理学のすべての領域で厳密に満たされていると仮定されています。 物理空間は、ユークリッド空間によって古典力学で表現される。

同様に、古典力学は、宇宙のすべての地域で同じように起こる絶対時間の存在を認め、それは物質的物体の存在と物理現象の発生とは無関係です。

考慮できる最も単純な移動体は、物質または粒子点である。 運動学では、この特定のモバイルケースが研究されるとき、それは粒子運動学と呼ばれ、研究中のモバイルが剛体であるとき、粒子のシステムおよび広範なアナログコンセプトとみなされ得る。 この場合、剛体または剛体の運動学と呼ばれます。

クラシックキネマティクスの基礎
キネマティクスは身体全体の動き、特に物質点の移動の単純化されたケースの研究を扱いますが、身体が動く理由を研究するのではなく、単に軌道を記述し、アドバンスで方向を変える方法を説明します。 多くの粒子系、例えば流体の場合、運動の法則は流体力学で研究されている。

パーティクルによって追跡される動きは、参照システムに関して観察者によって測定される。 数学的観点から、キネマティックは、粒子の位置の座標を時間に対してどのように変化させるかを表現する。 身体（または粒子）によって移動される軌道を記述する数学的関数は、速度（移動体が位置を変える速度）および加速度（時間に対する速度の変化）に依存する。

粒子（または剛体）の動きは、ベクトルの大きさである速度と加速度の値に基づいて記述できます。

加速度がゼロであれば、それは均一な直線運動を生じ、速度は時間の経過とともに一定のままである。

加速度が速度と同じ方向で一定であれば、それは均一に加速された直線運動を生じ、速度は時間とともに変化する。
加速度が速度に垂直な方向で一定であれば、速度のモジュラスが一定である均一な円運動を生じ、その方向を時間と共に変化させる。

加速度が一定で、速度および軌道と同じ平面にあるとき、放物線運動が起こり、加速方向の速度成分は均一に加速された直線運動として振る舞い、垂直成分Itは均一として振る舞う両方を構成するときには放物線の軌跡が生成されます。

加速度が一定であるが、速度および軌道と同一平面上にない場合、コリオリ効果が観察される。

単純調和運動では、振り子のような周期的な振動運動が存在し、体が一定の方向および等間隔で平衡位置から一方の側から他方の側へ振動する。 加速度および速度は関数であり、この場合は時間の正弦関数である。

剛体である場合、広大な物体の移動を考慮すると、粒子の移動方法を知ることで他の移動方法を推測することができます。 より具体的には：

2次元平面運動では、固体の2点の動きが分かっている場合、固体全体の動きが決定される

一般的な3次元移動では、固体の4点移動が分かっている場合に移動が決定される。

したがって、身体のある点、例えば身体の重心または他の任意の身体の重心を考慮すると、身体全体の動きは、

ここで：
 は、時刻tにおける身体上の点の位置である。
 は、時刻tにおける基準点（例えば、重心）の位置である。
 この行列を計算するために、基準点（または動きが平坦であれば1点以上）の他の3点の位置を知るのに十分であるとき、時刻tで身体の回りを回転する回転行列である。 。

回転運動の説明では、  身体が回転する回転軸と、回転軸に対する粒子の分布とを考慮する必要があります。 剛体の回転運動の研究は、剛体力学のテーマに含まれるのが普通である。  固有値1に関連して、各時点tにおいて回転軸が与えられる）。

興味深い動きは回転するトップの動きであり、回転すると歳差運動が起こる。 身体が平行移動や回転のような複数の動きを同時に持つ場合、それぞれに適した参照システムでそれぞれを個別に学習し、その動きを重ね合わせることができます。

座標系
動きの研究では、最も有用な座標系は、移動する経路の限界を見ているか、または動きに影響を与える加速度の幾何学的効果を分析しています。 したがって、円形のリングに沿って動くように強制されたかかとの動きを記述するために、最も有用な座標は、リング上でトレースされる角度である。 同じように、中心力の作用を受ける粒子の動きを記述するために、極座標が最も有用であろう。

大多数の場合、運動学的研究は、身体がたどる軌道に従って、1次元、2次元または3次元を用いてデカルト座標系で行われる。

移動記録
今日のテクノロジーは、身​​体によってもたらされる動きを記録するための多くの方法を提供しています。 したがって、車両の速度を測定するために、ドップラー効果に基づいた動作レーダーが利用可能である。 タコメータは、車輪の回転数に基づいて車両の速度を示す指標である。 歩行者は通路の特徴的な振動を検出する歩数計を有し、各ステップの特徴的な平均距離を仮定すると、移動距離を計算することができる。 ビデオは、画像のコンピュータ分析と共に、車両の位置および速度を決定することも可能にする。

動きの種類

直進運動
これは、移動体が直線軌道を描くものである。

均一な直線運動
この移動では、移動体は一定のV速度で直線に沿って移動する。 加速度aは常にゼロである。 これは、相互作用の外で宇宙に投げ込まれた物体の動き、または摩擦なしで滑る物体の動きに対応する。 速度Vが一定であるので、位置は、時間に関して直線的に変化する。

どこで  座標の中心に対する移動体の初期位置、すなわち  。

 前の方程式は、関数のグラフ表示で、原点を通過する線に対応する  。

一様に加速または変化する直進運動

この移動では、加速度は一定であるため、移動速度は線形に変化し、位置は時間と共に二次的に変化する。 この動きを支配する方程式は次のとおりです。

最終速度は、移動体の初期速度に時間の増加による加速度を足したものに等しい。  まあまあ：

最終速度は初期速度+時間に対する加速度に等しい。
速度を計算する関係から出発して：

どこで  、  初速度、あなたが持っている速度  、 我々は持っています。

加速度がゼロであれば、以前の方程式は一様な直線運動のもの、すなわち速度  定数。 残りの部分のボディ部分が均一に加速すると、  。

MRUAの2つの具体的なケースは自由落下と垂直撮影です。 自由落下は、地球の中心に向かって落下する重力の加速度（海面上の地球の場合、約9.8m / s 2）に相当する加速度で物体が動くことです。 一方、垂直方向のショットは、地球の中心と反対方向に投げられた物体の垂直方向のショットに対応し、高さを獲得する。 この場合、重力加速度は、オブジェクトを休止状態に達するまで、それを勝ち取る代わりに速度を失わせます。 そこから、初期速度ゼロの自由落下運動が始まる。

単純調和運動
これは、周期的な前後運動であり、一定の方向に均等な時間間隔で平衡位置のいずれかの側で振動する。 数学的に、移動するパスは、周期的な三角関数を使用して時間の関数として表されます。 たとえば、次元の移動の場合の時間に関する位置の式は、次のとおりです。

または

これは周波数正弦関数に対応する  振幅Aと初期位相  。

振り子の動き、ばねに付着した質量、または結晶格子内の原子の振動は、これらの特性のものです。

身体が経験する加速度は、物体の変位と、平衡点からの反対方向に比例する。 数学的に：

どこで  それは正の定数であり、  伸長（平衡位置からの身体の変位）を指す。

その微分方程式の解は、以前の形式の三角関数につながる。 論理的には、実際の周期的な周期的な動きは時間がたつにつれて減速します（主に摩擦）ので、加速の表現はより複雑であり、摩擦に関する新しい項を追加する必要があります。 現実の良い近似は、減衰振動運動の研究です。

放物線運動
放物線の動きは、2つの異なる直線運動の構成として解析することができます：一定速度の水平（x軸に沿った）と重力加速度で一様に加速されるもう1つの垂直（y軸による） 両方の組成が放物線状の軌道になる。
明らかに、速度の水平成分は変化しないままであるが、垂直成分および角度θは動きの過程で変化する。

初期速度ベクトル  初期角を形成する  x軸に関しては、 そして、分析のために、それは言及された2つのタイプの動きに分解される。 この分析の下で、初期速度のxおよびyに従う成分は、

水平変位は一様運動の法則によって与えられるため、その方程式は（

 ）：

軸に沿った移動  その方程式である直線的に均一に加速される。

あなたが置き換えて、位置を与える方程式で時間を無くすように動作するならば  そして xy平面内の軌道の方程式が得られる。

一般的な形をしている

平面y（x）における放物線を表している。 この表現は表示されていますが、その中には考慮されています  （それぞれのアニメーションではそうではありません）。 この図では、パラボリック軌道の最大高さがHで発生することが観察されています。速度の垂直成分  放物線の最大値はnullです。 水平の到達範囲  体が地面に戻ったときに起こります。  （ここで放物線は軸を切断する  ）。

円運動
円運動は実際には非常に一般的なタイプの動きです。例えば、回転するディスクの粒子、観覧車のもの、時計の手のもの、パレットのもの固定された軸の周りを回転するディスクの場合、その点のいずれかは、一定の時間間隔の間に特定の数のターンを実行する円形の軌道を記述する。 この動きの説明については、anglestoursを参照すると便利です。 後者はディスクのすべての点（同じ中心と呼ばれる）について同一であるからである。 ディスクの点によって移動される円弧の長さは、その位置に依存し、その距離だけ移動した角度と軸または回転中心との積に等しい。 角速度（ω）は、時間に対する角度変位として定義され、回転平面に垂直なベクトルによって表される。 その方向は「右手のルール」またはコルクスクリューを適用することによって決定される。 角加速度（α）は角速度の時間変化であり、角速度に近いベクトルで表されるが、同じ方向であってもなくてもよい（加速度または遅らせる）。
パーティクルの速度（v）は、モジュラスが単位時間当たりに移動した円弧の長さ（空間）を表すベクトルの大きさです。 前記モジュールは速度または速度とも呼ばれる。 それは、その方向が円形経路に接し、動きの方向と一致するベクトルによって表される。

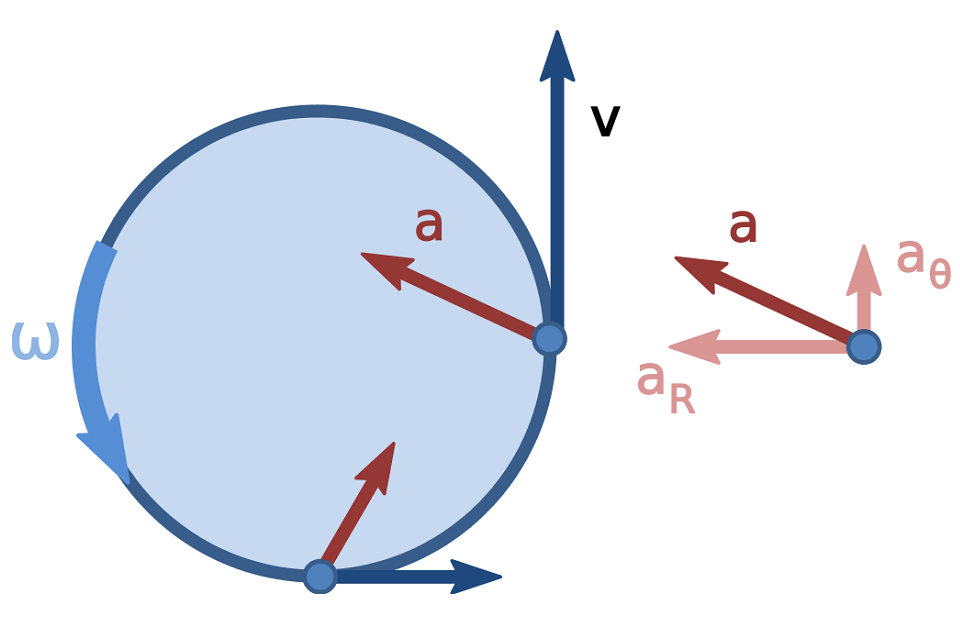
パーティクルの加速度（a）は、時間に対して速度が変化する速度を示すベクトルの大きさであり、単位時間当たりの速度ベクトルの変化である。 加速度は一般に2つの成分、すなわち軌道に接する加速度とそれに垂直な加速度である。 接線加速度は、時間に対する速度係数（速度）の変化を引き起こすものであり、通常の加速度は速度方向の変化に関与する。 両方の加速度成分のモジュールは、粒子が回転軸からの距離に依存する。

一様な円運動
それは、角加速度がゼロになるように可変速度または構造定数を有することを特徴とする。 粒子の線速度はモジュラスではなく方向に変化する。 接線加速度はゼロです。 方向変化の原因となる求心加速度（通常の加速）があります。
数学的には、角速度は次のように表される。

どこで  は角速度（定数）、  粒子によって掃引される角度の変化であり、  それは時間の変化です。 時間間隔内で移動した角度は次のとおりです。

均一に加速された円運動
この移動では、移動体が一定の角加速度を受けるため、角速度は時間に対して線形に変化する。 方程式は、均一に加速された直線のものと類似していますが、距離の代わりに角度を使用しています。 

であること  、一定角加速度。

複雑な高調波運動
それは、異なる方向の単純調和運動の組み合わせとして構成することができる二次元または三次元運動の一種である。 構造物が振動を受けた場合、特定の物質点の動きは、運動の振幅が小さい場合、しばしば複雑な調波運動によってモデル化することができる。

複雑なハーモニックムーブメントは、周期的な動きではなく、厳密に繰り返されることなくほぼサイクルを実行しますが、正確には決して繰り返されない準周期的な動きであるため興味深いです。この動きを実行する点のベクトル形式は次のようになります。

どこで  それらは空間の3つの方向における最大振幅であり、  発振周波数であり、  （初期条件は、振幅と位相の両方を計算することができる）。周波数はシステムの特性（質量、剛性など）に依存します。

一様な円運動は、実際には、2つの方向の振幅が円の半径に等しい複素調和運動の場合である  、2つの方向の周波数は一致する  特定のギャップの関係があります  。 振幅が等しくないか、または遅れが正確に与えられていない場合、この動きの軌跡が周波数は等しいが、結果は楕円運動である。

硬いソリッドな動き
上で説明したすべての動きは、具体的な物質点、すなわち小体、すなわち、軌道のサイズに関して小さい寸法を有する物理的な本体を指し、したがって物質点によって近似することができる。 しかし、巨視的な物理的な体は厳密ではないので、多くの状況において、体全体の動きは、そのすべての点が身体の点の間の距離よりもはるかに大きい軌道をたどると仮定することよりも複雑な記述を必要とする。物質点としての体は不十分であり、物質点の運動学は体の運動学を適切に記述するにはあまりにも単純である。 そのような場合には、身体の「軌道」が単純な3次元ユークリッド空間よりも複雑で豊かな空間を与えられる剛体の運動学が用いられなければならない。前記空間を通って前記本体を移動させるが、前記移動の際の前記本体の向きの変化を回転運動によって指定することを特徴とする方法。

差分計算を用いた数学的定式化
速度は位置ベクトルの時間微分であり、加速度は速度の時間微分である。

またはその積分式：

どこで  それらは初期条件です。

地球上での動き
気象学や発射体で大気などの体の動きを観測するとき、いわゆるコリオリ効果による偏差があります。 それらは、地球がその軸上を回転していることを証明するために使用されます。 映画的な観点からは、回転している参照系である地球の観測軌道を考えるときに何が起こるかを説明することは興味深い。

赤道の大砲が子午線に沿って北向きに射撃を発射したとする。 子午線の北に位置する観測者は、発射物が軌道の右にずれて予測される物の東に落下することを観察する。 同様に、発射体が南に沿って子午線に沿って発射した場合、発射体はまた、東方に逸脱し、この場合は軌道の左側に移動する。 コリオリ効果によって引き起こされるこの「偏差」の説明は、地球の回転によるものです。 発射体は3つの成分、すなわち、放物線状のショットに影響を与える2つの要素、すなわち北または南に向かう方向の2つの要素と、キャニオンを出る前の発射体による直前の要素に垂直な第3の要素赤道での地球の回転速度に等しい速度。 この回転速度の最後の要素は、地球の回転角速度が全面で一定ではあるが、赤道で最大で回転の線形回転ではなく、ポール。 したがって、発射体は北（または南）に向かって進み、地球の表面よりも東に向かってより速く動くので、言及された偏差が観察される。

地球上の別の興味深い運動の例は、フーコー振り子のものです。 振り子の振動面は固定されていませんが、北半球では時計回りに、南半球では反時計回りに回転しています。 振り子が赤道で振動すると、振動面は変化しません。 一方、極では、振動面の回転に1日かかります。 中位の緯度の場合は、緯度によって高い値をとります。 このようなターンの説明は、砲弾の発射と同じ原則に基づいている。

相対論的キネマティクス
相対性理論では、絶対的なものは空間や時間ではなく、真空中の光の速度です。 慣性基準システムの各観測者は、相対速度にかかわらず、別のシステムの別の観測者と同じ速度の光を測定します。これは古典的な観点からは不可能です。 2つの基準系間の運動の変換は、この事実を考慮しなければならず、そこからローレンツ変換が生じた。 彼らは、空間次元と時間が関連していることを示しているので、相対性理論では、時空と四次元空間について話すのは普通です。

相対論的効果の多くの実験的証拠がある。 例えば、光の速度に近い速度で生成された粒子の崩壊について実験室で測定された時間は、粒子が実験室に対して静止して生成されたときに測定された崩壊よりも高い。 これは、第1の場合に起こる相対論的時間的拡張によって説明される。

キネマティックスは、曲線の微分ジオメトリの特殊なケースで、すべてのカーブが同じ方法でパラメータ化されます。 相対論的なケースでは、座標時間は各観測者の相対的な尺度であるため、相対的な間隔として何らかのタイプの不変測度の使用が必要である。 観察者の座標時間と適切な時間との間の関係は、ローレンツ因子によって与えられる。