La théorie des cellules solaires explique le processus par lequel l’énergie lumineuse dans les photons est convertie en courant électrique lorsque les photons frappent un dispositif semi-conducteur approprié. Les études théoriques ont une utilité pratique car elles prédisent les limites fondamentales d’une cellule solaire et donnent des indications sur les phénomènes qui contribuent aux pertes et à l’efficacité des cellules solaires.

Explication simple
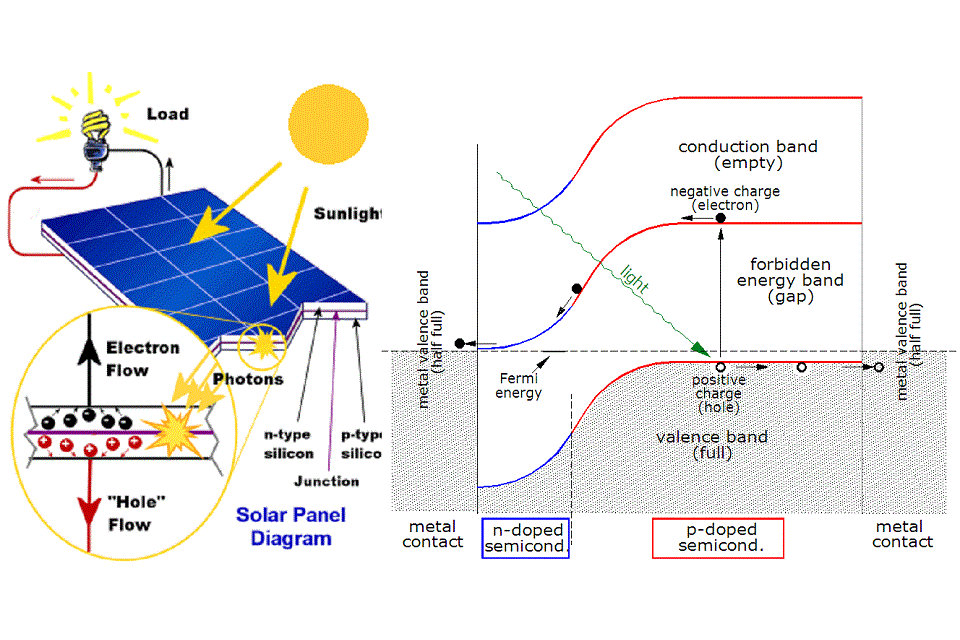
Les photons exposés au soleil frappent le panneau solaire et sont absorbés par des matériaux semi-conducteurs.

Les électrons (chargés négativement) sont détachés de leurs atomes lorsqu’ils sont excités. Grâce à leur structure particulière et aux matériaux des cellules solaires, les électrons ne peuvent que se déplacer dans une seule direction. La structure électronique des matériaux est très importante pour que le procédé fonctionne, et le silicium incorporant de petites quantités de bore ou de phosphore est souvent utilisé dans différentes couches.

Un ensemble de cellules solaires convertit l’énergie solaire en une quantité utilisable d’électricité à courant continu (DC).

Photogénération de porteurs de charge
Lorsqu’un photon frappe un morceau de silicium, trois choses peuvent se produire:
Le photon peut traverser directement le silicium, ce qui se produit généralement pour les photons de faible énergie.

Le photon peut réfléchir sur la surface.
Le photon peut être absorbé par le silicium si l’énergie des photons est supérieure à la valeur de la bande interdite du silicium. Cela génère une paire électron-trou et parfois de la chaleur en fonction de la structure de la bande.

Lorsqu’un photon est absorbé, son énergie est transmise à un électron dans le réseau cristallin.Habituellement, cet électron est dans la bande de valence. L’énergie donnée à l’électron par le photon l’excite dans la bande de conduction où elle est libre de se déplacer dans le semi-conducteur.Le réseau de liaisons covalentes dont l’électron faisait auparavant partie a un électron de moins.Ceci est connu comme un trou. La présence d’une liaison covalente manquante permet aux électrons liés des atomes voisins de se déplacer dans le « trou », laissant un autre trou derrière, propageant ainsi des trous dans tout le réseau. On peut dire que les photons absorbés dans le semi-conducteur créent des paires électron-trou.

Un photon doit uniquement avoir une énergie supérieure à celle de la bande interdite pour exciter un électron de la bande de valence dans la bande de conduction. Cependant, le spectre de la fréquence solaire approche un spectre de corps noir d’environ 5 800 K et, par conséquent, une grande partie du rayonnement solaire atteignant la Terre est composée de photons dont l’énergie est supérieure à la bande interdite du silicium. Ces photons à énergie plus élevée seront absorbés par la cellule solaire, mais la différence d’énergie entre ces photons et la bande interdite de silicium est convertie en chaleur (via des vibrations de réseau appelées phonons) plutôt qu’en énergie électrique utilisable. L’effet photovoltaïque peut également se produire lorsque deux photons sont absorbés simultanément dans un processus appelé effet photovoltaïque à deux photons. Cependant, des intensités optiques élevées sont requises pour ce processus non linéaire.

La jonction pn
La cellule solaire la plus connue est configurée comme une jonction pn de grande surface en silicium. Pour simplifier, on peut imaginer amener une couche de silicium de type n en contact direct avec une couche de silicium de type p. En pratique, les jonctions pn des cellules solaires au silicium ne sont pas fabriquées de cette manière, mais plutôt en diffusant un dopant de type n sur un côté d’une plaquette de type p (ou vice versa).

Si un morceau de silicium de type p est placé en contact étroit avec un morceau de silicium de type n, une diffusion des électrons se produit de la région de forte concentration d’électrons (côté n de la jonction) dans la région de faible intensité. concentration d’électrons (côté de type p de la jonction).Lorsque les électrons diffusent à travers la jonction pn, ils se recombinent avec des trous du côté p.Cependant (en l’absence de circuit externe), cette diffusion des porteurs ne se poursuit pas indéfiniment car des charges s’accumulent de part et d’autre de la jonction et créent un champ électrique. Le champ électrique favorise le flux de charge, appelé courant de dérive, qui s’oppose et finit par compenser la diffusion des électrons et des trous. Cette région où les électrons et les trous ont diffusé à travers la jonction s’appelle la région d’appauvrissement car elle ne contient pratiquement pas de porteurs de charge mobiles. Il est également connu sous le nom de région de charge d’espace, bien que la charge d’espace s’étende un peu plus loin dans les deux directions que la région d’appauvrissement.

Séparation des porteurs de charge
Il existe deux causes de mouvement et de séparation des porteurs de charge dans une cellule solaire:
dérive des porteurs, entraînée par le champ électrique, les électrons étant poussés dans un sens et les trous dans l’autre sens

diffusion de porteurs de zones de plus forte concentration en porteurs vers des zones de plus faible concentration en porteurs (suivant un gradient de potentiel électrochimique).

Ces deux « forces » peuvent travailler l’une contre l’autre à n’importe quel endroit de la cellule. Par exemple, un électron se déplaçant à travers la jonction de la région p vers la région n (comme dans le diagramme au début de cet article) est poussé par le champ électrique contre le gradient de concentration. La même chose vaut pour un trou qui se déplace dans la direction opposée.

Il est plus facile de comprendre comment un courant est généré lors de la prise en compte des paires électron-trou créées dans la zone d’appauvrissement, où se trouve un fort champ électrique.L’électron est poussé par ce champ vers le côté n et le trou vers le côté p. (Ceci est opposé à la direction du courant dans une diode polarisée en direct, telle qu’une diode électroluminescente en fonctionnement.) Lorsque la paire est créée en dehors de la zone de charge spatiale, où le champ électrique est plus petit, la diffusion agit également les porteurs, mais la jonction joue toujours un rôle en balayant les électrons qui l’atteignent du côté p vers le côté n et en balayant les trous qui l’atteignent du côté n vers le côté p, créant ainsi un gradient de concentration à zone de charge d’espace.

Dans les cellules solaires épaisses, il y a très peu de champ électrique dans la région active en dehors de la zone de charge spatiale, de sorte que le mode dominant de séparation des porteurs de charge est la diffusion. Dans ces cellules, la longueur de diffusion des porteurs minoritaires (la longueur que les porteurs photo-générés peuvent parcourir avant de se recombiner) doit être importante par rapport à l’épaisseur de la cellule. Dans les cellules à couche mince (telles que le silicium amorphe), la longueur de diffusion des porteurs minoritaires est généralement très courte du fait de l’existence de défauts et la séparation de charge dominante est donc dérivée par le champ électrostatique de la jonction. épaisseur totale de la cellule.

Une fois que le transporteur minoritaire pénètre dans la région de la dérive, il est «balayé» à travers la jonction et, de l’autre côté de la jonction, devient un transporteur majoritaire. Ce courant inverse est un courant de génération, alimenté à la fois thermiquement et (le cas échéant) par l’absorption de la lumière. D’autre part, les porteurs majoritaires sont entraînés dans la région de dérive par diffusion (résultant du gradient de concentration), ce qui conduit au courant direct; seuls les porteurs majoritaires avec les énergies les plus élevées (dans la queue dite de Boltzmann; cf. statistiques de Maxwell – Boltzmann) peuvent traverser complètement la région de dérive. Par conséquent, la distribution de la porteuse dans l’ensemble du dispositif est régie par un équilibre dynamique entre le courant inverse et le courant direct.

Connexion à une charge externe
Les contacts ohmiques métal-semiconducteur sont réalisés à la fois sur les côtés de type n et de type p de la cellule solaire et sur les électrodes connectées à une charge externe. Les électrons créés du côté du type n, ou créés du côté du type p, « collectés » par la jonction et balayés sur le côté du type n, peuvent traverser le fil, alimenter la charge et continuer à travers le fil jusqu’à ce qu’ils atteignent le contact semi-conducteur en métal de type p. Ici, ils se recombinent avec un trou qui a été soit créé comme une paire électron-trou sur le côté de type p de la cellule solaire, ou un trou qui a été balayé à travers la jonction du côté de type n après avoir été créé là.

La tension mesurée est égale à la différence entre les niveaux de quasi-fermi des porteurs majoritaires (électrons dans la partie de type n et trous dans la partie de type p) aux deux bornes.

Circuit équivalent d’une cellule solaire
Pour comprendre le comportement électronique d’une cellule solaire, il est utile de créer un modèle électriquement équivalent, basé sur des composants électriques idéaux discrets dont le comportement est bien défini. Une cellule solaire idéale peut être modélisée par une source de courant en parallèle avec une diode; en pratique, aucune cellule solaire n’est idéale, de sorte qu’une résistance de shunt et un composant de résistance série sont ajoutés au modèle. Le circuit équivalent résultant d’une cellule solaire est montré à gauche. La représentation schématique d’une cellule solaire à utiliser dans les schémas de circuit est également illustrée à droite.

Équation caractéristique
À partir du circuit équivalent, il est évident que le courant produit par la cellule solaire est égal à celui produit par la source de courant, moins celui qui traverse la diode, moins celui qui traverse la résistance de shunt:

où
I = courant de sortie (ampère)
I _L = courant photogénéré (ampère)
I _D = courant de diode (ampère)
I _SH = courant de dérivation (ampère).

Le courant traversant ces éléments est régi par la tension qui les traverse:

où
V _j = tension aux bornes de la diode et de la résistance RSH (volt)
V = tension aux bornes de sortie (volt)
I = courant de sortie (ampère)
R _S = résistance série (Ω).

Par l’équation de la diode Shockley, le courant dévié à travers la diode est:

où
I ₀ = courant de saturation inverse (ampère)
n = facteur d’idéalité de la diode (1 pour une diode idéale)
q = charge élémentaire
k = constante de Boltzmann
T = température absolue

 la tension thermique. À 25 ° C,  volt.
Par la loi d’Ohm, le courant dévié par la résistance de shunt est:

où
R _SH = résistance shunt (Ω).

En les substituant dans la première équation, on obtient l’équation caractéristique d’une cellule solaire, qui relie les paramètres des cellules solaires au courant et à la tension de sortie:

Une dérivation alternative produit une équation similaire en apparence, mais avec V sur le côté gauche. Les deux alternatives sont les identités; c’est-à-dire qu’ils donnent exactement les mêmes résultats.

Puisque les paramètres I ₀ , n, R _S et R _SH ne peuvent pas être mesurés directement, l’application la plus courante de l’équation caractéristique est la régression non linéaire pour extraire les valeurs de ces paramètres en fonction de leur effet combiné sur le comportement des cellules solaires.

Lorsque R _S n’est pas nul, l’équation ci-dessus ne donne pas directement le courant I, mais elle peut alors être résolue en utilisant la fonction Lambert W:

Lorsqu’une charge externe est utilisée avec la cellule, sa résistance peut simplement être ajoutée à RS et V réglée à zéro afin de trouver le courant.

Lorsque R _SH est infini, il existe une solution pour V pour tout  moins que  :

Sinon, on peut résoudre V en utilisant la fonction Lambert W:

Cependant, lorsque R _SH est grand, il est préférable de résoudre l’équation d’origine numériquement.
La forme générale de la solution est une courbe avec I décroissant lorsque V augmente. La pente à petit ou négatif V (où la fonction W est proche de zéro) approche  , alors que la pente à haute V approche  .

Tension en circuit ouvert et courant de court-circuit
Lorsque la cellule est utilisée en circuit ouvert, I = 0 et la tension aux bornes de sortie est définie comme la tension à vide . En supposant que la résistance de shunt est suffisamment élevée pour négliger le terme final de l’équation caractéristique, la tension en circuit ouvert V _OC est:

De même, lorsque la cellule est utilisée en court-circuit, V = 0 et le courant I traversant les bornes est défini comme le courant de court-circuit. On peut montrer que pour une cellule solaire de haute qualité (faible R _S et I ₀ , et haute R _SH ), le courant de court-circuit I _SC est:

Il n’est pas possible d’extraire de l’alimentation de l’appareil lorsqu’il fonctionne en circuit ouvert ou en court-circuit.

Effet de la taille physique
Les valeurs de IL, I0, RS et RSH dépendent de la taille physique de la cellule solaire. En comparant des cellules par ailleurs identiques, une cellule avec deux fois la zone de jonction d’un autre aura, en principe, le double de IL et I0, car elle a deux fois la zone de photocourant et le courant de diode peut circuler. Par le même argument, il aura également la moitié de la RS de la résistance série liée au flux de courant vertical; cependant, pour les cellules solaires au silicium de grande surface, la mise à l’échelle de la résistance série rencontrée par le flux de courant latéral n’est pas facilement prévisible puisqu’elle dépendra essentiellement de la conception du réseau (on ne sait pas ce que « autrement identique » signifie à cet égard). Selon le type de shunt, la plus grande cellule peut également avoir la moitié du RSH, car elle a deux fois la zone où les shunts peuvent se produire; Par contre, si des shunts se produisent principalement au périmètre, le RSH diminuera en fonction du changement de circonférence et non de la surface.

Étant donné que les changements dans les courants sont les principaux et s’équilibrent, la tension à vide est pratiquement la même; Le COV commence à dépendre de la taille de la cellule uniquement si le RSH devient trop faible. Pour tenir compte de la dominance des courants, l’équation caractéristique est fréquemment écrite en termes de densité de courant ou de courant produit par unité de surface cellulaire:

où
J = densité de courant (ampère / cm ² )
J _L = densité de courant photogénérée (ampère / cm ² )
J ₀ = densité de courant de saturation inverse (ampère / cm ² )
r _S = résistance série spécifique (Ω-cm ² )
r _SH = résistance spécifique au shunt (Ω-cm ² ).

Cette formulation présente plusieurs avantages. La première est que, puisque les caractéristiques des cellules sont référencées dans une zone transversale commune, elles peuvent être comparées pour des cellules de différentes dimensions physiques. Bien que cela présente un avantage limité dans un contexte de fabrication, où toutes les cellules ont tendance à avoir la même taille, cela est utile dans la recherche et dans la comparaison des cellules entre les fabricants. Un autre avantage est que l’équation de densité met naturellement à l’échelle les valeurs des paramètres à des ordres de grandeur similaires, ce qui peut en rendre l’extraction numérique plus simple et plus précise, même avec des méthodes de résolution naïves.

Il existe des limitations pratiques de cette formulation. Par exemple, certains effets parasites prennent de plus en plus d’importance à mesure que la taille des cellules diminue et peuvent affecter les valeurs de paramètres extraites. La recombinaison et la contamination de la jonction ont tendance à être plus grandes au périmètre de la cellule, de sorte que de très petites cellules peuvent présenter des valeurs plus élevées de J0 ou des valeurs plus faibles de RSH que des cellules plus grandes qui sont identiques. Dans de tels cas, les comparaisons entre les cellules doivent être effectuées avec prudence et en tenant compte de ces effets.
Cette approche ne doit être utilisée que pour comparer des cellules solaires à disposition comparable. Par exemple, une comparaison entre des cellules solaires principalement quadratiques telles que les cellules solaires au silicium cristallin et les cellules solaires étroites mais longues comme les cellules solaires à couches minces typiques peut conduire à des hypothèses erronées dues aux différents types de cheminement et donc une contribution de résistance série distribuée à rS. La macro-architecture des cellules solaires pourrait entraîner la mise en place de différentes surfaces sur n’importe quel volume fixe, en particulier pour les cellules solaires à couches minces et les cellules solaires flexibles, ce qui pourrait permettre des structures pliées fortement convolutées.Si le volume est la contrainte de liaison, la densité d’efficacité basée sur la surface peut être moins pertinente.

Electrodes conductrices transparentes
Les électrodes conductrices transparentes sont des composants essentiels des cellules solaires. Il s’agit soit d’un film continu d’oxyde d’indium et d’étain, soit d’un réseau de fils conducteurs, dans lequel les fils sont des collecteurs de charge tandis que les vides entre les fils sont transparents pour la lumière. Une densité optimale du réseau de fils est essentielle pour la performance maximale des cellules solaires, car une densité de fils plus élevée bloque la transmittance de la lumière alors qu’une densité de fils inférieure entraîne des pertes de recombinaison élevées dues à la distance parcourue par les porteurs de charge.

Température de la cellule
La température affecte l’équation caractéristique de deux manières: directement, via T dans le terme exponentiel, et indirectement via son effet sur I0 (à proprement parler, la température affecte tous les termes, mais ceux-ci sont beaucoup plus significatifs que les autres). Tandis que l’augmentation de T réduit l’amplitude de l’exposant dans l’équation caractéristique, la valeur de I0 augmente de façon exponentielle avec T. L’effet net est de réduire de manière linéaire les COV (la tension en circuit ouvert) lorsque la température augmente. L’ampleur de cette réduction est inversement proportionnelle à celle des COV; c’est-à-dire que les cellules avec des valeurs de COV plus élevées subissent des réductions de tension plus faibles lorsque la température augmente. Pour la plupart des cellules solaires en silicium cristallin, la variation de la teneur en COV avec la température est d’environ -0,50% / ° C, bien que la vitesse pour les cellules de silicium cristallin les plus efficaces soit d’environ -0,35% / ° C. A titre de comparaison, le taux pour les cellules solaires en silicium amorphe est de -0,20% / ° C à -0,30% / ° C, en fonction de la fabrication de la cellule.

La quantité de courant photogénéré IL augmente légèrement avec l’augmentation de la température en raison d’une augmentation du nombre de porteurs générés thermiquement dans la cellule. Cet effet est toutefois faible: environ 0,065% / ° C pour les cellules de silicium cristallin et 0,09% pour les cellules de silicium amorphe.

L’effet global de la température sur l’efficacité des cellules peut être calculé en utilisant ces facteurs en combinaison avec l’équation caractéristique. Cependant, comme le changement de tension est beaucoup plus fort que le changement de courant, l’effet global sur l’efficacité tend à être similaire à celui de la tension. Le rendement de la plupart des cellules solaires en silicium cristallin diminue de 0,50% / ° C et la plupart des cellules amorphes diminuent de 0,15-0,25% / ° C. La figure ci-dessus montre des courbes IV que l’on peut généralement voir pour une cellule solaire en silicium cristallin à différentes températures.

Résistance série
À mesure que la résistance série augmente, la chute de tension entre la tension de jonction et la tension aux bornes devient plus grande pour le même courant. Le résultat est que la partie contrôlée par le courant de la courbe IV commence à s’affaisser vers l’origine, produisant une diminution significative de la tension terminale  et une légère réduction de l’ISC, le courant de court-circuit.Des valeurs très élevées de RS produiront également une réduction significative de l’ISC; dans ces régimes, la résistance des séries domine et le comportement de la cellule solaire ressemble à celui d’une résistance. Ces effets sont présentés pour les cellules solaires en silicium cristallin dans les courbes IV affichées sur la figure à droite.

Les pertes causées par la résistance en série sont en première approximation données par la _{perte de}P = V _Rs I = I ² R _S et augmentent de manière quadratique avec le (photo) courant. Les pertes de résistance en série sont donc les plus importantes pour les intensités d’éclairage élevées.

Résistance de shunt
Lorsque la résistance de shunt diminue, le courant dévié à travers la résistance de shunt augmente pour un niveau donné de tension de jonction. Le résultat est que la partie contrôlée par la tension de la courbe IV commence à s’affaisser loin de l’origine, produisant une diminution significative du courant terminal I et une légère réduction des COV. Des valeurs très faibles de RSH produiront une réduction significative des COV. Tout comme dans le cas d’une résistance série élevée, une cellule solaire à faible shunt prend des caractéristiques de fonctionnement similaires à celles d’une résistance. Ces effets sont présentés pour les cellules solaires en silicium cristallin dans les courbes IV affichées sur la figure à droite.

Courant de saturation inverse
Si l’on suppose une résistance de shunt infinie, l’équation caractéristique peut être résolue pour V _OC:

Ainsi, une augmentation de I0 produit une réduction de COV proportionnelle à l’inverse du logarithme de l’augmentation. Ceci explique mathématiquement la raison de la réduction des COV qui accompagne les augmentations de température décrites ci-dessus. L’effet du courant de saturation inverse sur la courbe IV d’une cellule solaire en silicium cristallin est montré dans la figure à droite. Physiquement, le courant de saturation inverse est une mesure de la « fuite » des porteurs à travers la jonction pn en polarisation inverse. Cette fuite résulte de la recombinaison de la porteuse dans les régions neutres de chaque côté de la jonction.

Facteur d’idéalité
Le facteur d’idéalité (également appelé facteur d’émissivité) est un paramètre approprié qui décrit dans quelle mesure le comportement de la diode correspond à celui prédit par la théorie, qui suppose que la jonction pn de la diode est un plan infini et qu’aucune recombinaison Une correspondance parfaite avec la théorie est indiquée lorsque n = 1. Lorsque la recombinaison dans la région de charge d’espace domine une autre recombinaison, cependant, n = 2. L’effet de la variation du facteur d’idéalité indépendamment de tous les autres paramètres est montré pour une cellule solaire en silicium cristallin. les courbes IV affichées dans la figure à droite.

La plupart des cellules solaires, qui sont assez grandes par rapport aux diodes conventionnelles, se rapprochent bien d’un plan infini et présentent généralement un comportement quasi idéal selon les conditions d’essai standard (n ≈ 1). Dans certaines conditions de fonctionnement, cependant, le fonctionnement du dispositif peut être dominé par la recombinaison dans la région de charge d’espace. Cela se caractérise par une augmentation significative de I0 ainsi qu’une augmentation du facteur d’idéalité à n n 2. Ce dernier tend à augmenter la tension de sortie des cellules solaires tandis que le premier agit pour l’éroder. L’effet net est donc une combinaison de l’augmentation de la tension indiquée pour l’augmentation de n dans la figure à droite et de la diminution de la tension indiquée pour augmenter I0 dans la figure ci-dessus. En règle générale, I0 est le facteur le plus important et il en résulte une réduction de la tension.

On observe parfois que le facteur d’idéalité est supérieur à 2, ce qui est généralement attribué à la présence d’une diode Schottky ou d’une hétérojonction dans la cellule solaire. La présence d’un décalage d’hétérojonction réduit l’efficacité de la collecte de la cellule solaire et peut contribuer à un faible facteur de remplissage.