La cinématique est la branche de la physique qui décrit le mouvement des objets solides sans tenir compte des causes qui en sont à l’origine (les forces) et qui se limite principalement à l’étude de l’histoire en fonction du temps. Pour cela, il utilise des vitesses et des accélérations décrivant l’évolution de la position en fonction du temps. La vitesse est déterminée comme le quotient entre le déplacement et le temps utilisé, tandis que l’accélération est le quotient entre le changement de vitesse et le temps utilisé.

Éléments de base de la cinématique
Les éléments de base de la cinématique sont l’espace, le temps et un mobile.

En mécanique classique, on admet l’existence d’un espace absolu, c’est-à-dire un espace antérieur à tous les objets matériels et indépendant de leur existence. Cet espace est le stade où se produisent tous les phénomènes physiques, et on suppose que toutes les lois de la physique sont rigoureusement remplies dans toutes les régions de la physique. L’espace physique est représenté dans la mécanique classique au moyen d’un espace euclidien.

De manière analogue, la mécanique classique admet l’existence d’un temps absolu qui se déroule de la même manière dans toutes les régions de l’univers et qui est indépendant de l’existence d’objets matériels et de l’occurrence de phénomènes physiques.

Le mobile le plus simple à prendre en compte est le matériau ou le point particulaire; lorsque, dans la cinématique, ce cas particulier de mobile est étudié, il est appelé cinématique de particules, et lorsque le mobile à l’étude est un corps rigide, il peut être considéré comme un système de particules et de concepts analogiques étendus; dans ce cas, on parle de cinématique du solide rigide ou du corps rigide.

Fondation de la cinématique classique
La cinématique traite de l’étude du mouvement des corps en général et, en particulier, du cas simplifié du mouvement d’un point matériel, mais n’étudie pas pourquoi les corps bougent mais décrit simplement leurs trajectoires et comment se réorienter dans leur progression. Pour de nombreux systèmes de particules, par exemple les fluides, les lois du mouvement sont étudiées en mécanique des fluides.

Le mouvement tracé par une particule est mesuré par un observateur par rapport à un système de référence. Du point de vue mathématique, la cinématique exprime la variation de la position de la / des particule (s) en fonction du temps. La fonction mathématique qui décrit la trajectoire parcourue par le corps (ou la particule) dépend de la vitesse (la vitesse à laquelle un mobile change de position) et de l’accélération (variation de la vitesse en fonction du temps).

Le mouvement d’une particule (ou d’un corps rigide) peut être décrit en fonction des valeurs de vitesse et d’accélération, qui sont des grandeurs vectorielles:

Si l’accélération est nulle, il en résulte un mouvement rectiligne uniforme et la vitesse reste constante dans le temps.

Si l’accélération est constante dans le même sens que la vitesse, le mouvement rectiligne est uniformément accéléré et la vitesse varie avec le temps.
Si l’accélération est constante avec une direction perpendiculaire à la vitesse, il en résulte un mouvement circulaire uniforme, où le module de la vitesse est constant, changeant de direction avec le temps.

Lorsque l’accélération est constante et se situe dans le même plan que la vitesse et la trajectoire, il se produit un mouvement parabolique, où la composante de la vitesse dans la direction de l’accélération se comporte comme un mouvement rectiligne uniformément accéléré, et la composante perpendiculaire Il se comporte comme une uniformité mouvement rectiligne et une trajectoire parabolique est générée lors de la composition des deux.

Lorsque l’accélération est constante mais pas dans le même plan que la vitesse et la trajectoire, l’effet Coriolis est observé.

Dans le mouvement harmonique simple, il existe un mouvement oscillant périodique, semblable à celui du pendule, dans lequel un corps oscille d’un côté à l’autre de la position d’équilibre dans une certaine direction et à des intervalles de temps égaux. L’accélération et la vitesse sont des fonctions, dans ce cas, sinusoïdales du temps.

Quand on considère le mouvement de translation d’un corps étendu, dans le cas d’un corps rigide, en sachant comment l’une des particules se déplace, on en déduit comment les autres se déplacent.Plus concrètement:

Dans un mouvement plan en deux dimensions, si le mouvement du solide en 2 points est connu, le mouvement de tout le solide est déterminé

Dans un mouvement tridimensionnel général, le mouvement est déterminé si le mouvement du solide en 4 points est connu.

Ainsi, en considérant une pointe du corps, par exemple le centre de gravité du corps ou tout autre, le mouvement de tout le corps peut être exprimé par:

où:
 , est la position d’un point sur le corps au temps t.
 , est la position du point de référence (par exemple le centre de gravité) à l’instant t.
 , est une matrice de rotation qui prend en compte la rotation du corps autour de lui-même au temps t, pour calculer cette matrice, il suffit de connaître la position de 3 autres points en plus du point de référence (ou 1 point de plus si le mouvement est plat) .

Dans la description du mouvement de rotation donné par  il faut considérer l’axe de rotation par rapport auquel le corps tourne et la répartition des particules par rapport à l’axe de rotation.L’étude du mouvement de rotation d’un solide rigide est généralement incluse dans le thème de la mécanique des solides rigides, car elle est plus compliquée (la direction principale de associée à la valeur propre 1, donne l’axe de rotation à chaque instant t).

Un mouvement intéressant est celui d’une toupie qui, en tournant, peut avoir un mouvement de précession et de nutation. Lorsqu’un corps a plusieurs mouvements simultanément, tels qu’un mouvement de translation et un mouvement de rotation, vous pouvez les étudier séparément dans le système de référence approprié à chacun d’eux, puis les superposer.

Systèmes de coordonnées
Dans l’étude du mouvement, les systèmes de coordonnées les plus utiles sont la visualisation des limites du chemin à parcourir ou l’analyse de l’effet géométrique de l’accélération affectant le mouvement. Ainsi, pour décrire le mouvement d’un talon contraint de se déplacer le long d’un anneau circulaire, la coordonnée la plus utile serait l’angle tracé sur l’anneau. De même, pour décrire le mouvement d’une particule soumise à l’action d’une force centrale, les coordonnées polaires seraient les plus utiles.

Dans la grande majorité des cas, l’étude cinématique est réalisée sur un système de coordonnées cartésiennes, à une, deux ou trois dimensions, selon la trajectoire suivie par le corps.

Enregistrement de mouvement
La technologie actuelle nous offre de nombreuses façons d’enregistrer le mouvement effectué par un corps. Ainsi, pour mesurer la vitesse des véhicules, il existe un radar de trafic dont le fonctionnement est basé sur l’effet Doppler. Le tachymètre est un indicateur de la vitesse d’un véhicule en fonction de la fréquence de rotation des roues. Les marcheurs disposent de podomètres qui détectent les vibrations caractéristiques du passage et permettent, en supposant une distance moyenne caractéristique pour chaque pas, de calculer la distance parcourue. La vidéo, associée à l’analyse informatique des images, permet également de déterminer la position et la vitesse des véhicules.

Types de mouvements

Mouvement rectiligne
C’est celui dans lequel le mobile décrit une trajectoire en ligne droite.

Mouvement rectiligne uniforme
Dans ce mouvement, le mobile se déplace le long d’une ligne droite à une vitesse V constante;l’accélération a est égale à zéro tout le temps. Cela correspond au mouvement d’un objet jeté dans l’espace en dehors de toute interaction, ou au mouvement d’un objet qui glisse sans frottement.Puisque la vitesse V est constante, la position variera linéairement par rapport au temps, selon l’équation:

où  est la position initiale du mobile par rapport au centre de coordonnées, c’est-à-dire pour  .

 l’équation précédente correspond à une ligne passant par l’origine, dans une représentation graphique de la fonction  .

Mouvement rectiligne uniformément accéléré ou varié

Dans ce mouvement, l’accélération est constante, de sorte que la vitesse du mobile varie linéairement et la position de manière quadratique avec le temps. Les équations qui régissent ce mouvement sont les suivantes:

la vitesse finale est égale à la vitesse initiale du mobile plus l’accélération due à l’augmentation du temps.  Comme ci comme ça:

la vitesse finale est égale à la vitesse initiale plus l’accélération temporelle.
A partir de la relation qui calcule la vitesse:

Où  ,  la vitesse initiale, celle que vous avez pour  , on a.

Notez que si l’accélération était nulle, les équations précédentes correspondraient à celles d’un mouvement rectiligne uniforme, c’est-à-dire avec la vitesse.  constant. Si la partie du corps du reste accélère uniformément, le  .

Deux cas spécifiques de MRUA sont la chute libre et la prise de vue verticale. La chute libre est le mouvement d’un objet qui tombe vers le centre de la Terre avec une accélération équivalente à l’accélération de la pesanteur (qui dans le cas de la planète Terre au niveau de la mer est d’environ 9,8 m / s 2). Le tir vertical, en revanche, correspond à celui d’un objet lancé dans la direction opposée au centre de la Terre, prenant de la hauteur. Dans ce cas, l’accélération de la gravité provoque la perte de vitesse de l’objet, au lieu de la gagner, jusqu’à atteindre l’état de repos; puis, et à partir de là, commence un mouvement de chute libre avec une vitesse initiale nulle.

Mouvement harmonique simple
Il s’agit d’un mouvement de va-et-vient périodique dans lequel un corps oscille de part et d’autre d’une position d’équilibre dans une certaine direction et à des intervalles de temps égaux.Mathématiquement, le chemin parcouru est exprimé en fonction du temps à l’aide de fonctions trigonométriques périodiques. Par exemple, l’équation de position par rapport au temps, dans le cas d’un mouvement dans une dimension est:

ou

qui correspond à une fonction sinusoïdale de fréquence  ,, amplitude A et phase initiale  .

Les mouvements du pendule, d’une masse attachée à un ressort ou la vibration des atomes dans les réseaux cristallins sont de ces caractéristiques.

L’accélération ressentie par le corps est proportionnelle au déplacement de l’objet et à la direction opposée, à partir du point d’équilibre. Mathématiquement:

où  c’est une constante positive et  , fait référence à l’allongement (déplacement du corps à partir de la position d’équilibre).

La solution à cette équation différentielle conduit à des fonctions trigonométriques de la forme précédente. Logiquement, un véritable mouvement périodique oscillatoire ralentit dans le temps (principalement des frictions), de sorte que l’expression de l’accélération est plus compliquée, nécessitant l’ajout de nouveaux termes liés à la friction. Une bonne approximation de la réalité est l’étude du mouvement oscillatoire amorti.

Mouvement parabolique
Le mouvement parabolique peut être analysé comme la composition de deux mouvements rectilignes différents: un horizontal (selon l’axe des x) à vitesse constante et un autre vertical (selon l’axe des y) uniformément accéléré, avec l’accélération gravitationnelle; la composition des deux entraîne une trajectoire parabolique.
Clairement, la composante horizontale de la vitesse reste inchangée, mais la composante verticale et l’angle 0 changent au cours du mouvement.

Le vecteur de vitesse initiale  forme un angle initial  par rapport à l’axe des x ; et, comme dit, pour l’analyse, il est divisé en deux types de mouvement mentionnés; Sous cette analyse, les composantes selon x et y de la vitesse initiale seront:

Le déplacement horizontal est donné par la loi du mouvement uniforme, donc ses équations seront (si on considère

 ):

Tant que le mouvement selon l’axe  sera rectiligne uniformément accéléré, étant ses équations:

Si vous remplacez et opérez pour éliminer le temps, avec les équations qui donnent les positions  et  , l’équation de la trajectoire dans le plan xy est obtenue:

qui a la forme générale

et représente une parabole dans le plan y (x). Cette représentation est montrée, mais dans elle a été considérée  (pas si dans l’animation respective). Sur cette figure, on observe également que la hauteur maximale dans la trajectoire parabolique se produira dans H, lorsque la composante verticale de la vitesse  est nul (maximum de la parabole); et que la portée horizontale  se produira lorsque le corps retourne au sol, dans  (où la parabole coupe l’axe  ).

Mouvement circulaire
Le mouvement circulaire est en pratique un type de mouvement très courant: ils le connaissent, par exemple, les particules d’un disque qui tourne sur son axe, celles d’une grande roue, celles des aiguilles d’une horloge, celles des palettes de un ventilateur, etc. Dans le cas d’un disque tournant autour d’un axe fixe, l’un quelconque de ses points décrit des trajectoires circulaires, effectuant un certain nombre de tours pendant un certain intervalle de temps. Pour la description de ce mouvement, il est commode de se référer à Anglestours; puisque ces derniers sont identiques pour tous les points du disque (référés au même centre). La longueur de l’arc parcouru par une pointe du disque dépend de sa position et est égale au produit de l’angle parcouru par sa distance par rapport à l’axe ou au centre de rotation. La vitesse angulaire () est définie comme le déplacement angulaire par rapport au temps et est représentée par un vecteur perpendiculaire au plan de rotation; sa direction est déterminée en appliquant la « règle de la main droite » ou le tire-bouchon. L’accélération angulaire (α) s’avère être une variation de la vitesse angulaire par rapport au temps, elle est représentée par un vecteur analogue à celui de la vitesse angulaire, mais elle peut avoir ou non la même direction (selon qu’elle accélère ou non). ou retarde).
La vitesse (v) d’une particule est une grandeur vectorielle dont le module exprime la longueur de l’arc parcouru (espace) par unité de temps; ledit module est également appelé vitesse ou célérité. Il est représenté par un vecteur dont la direction est tangente à la trajectoire circulaire et coïncide avec celle du mouvement.

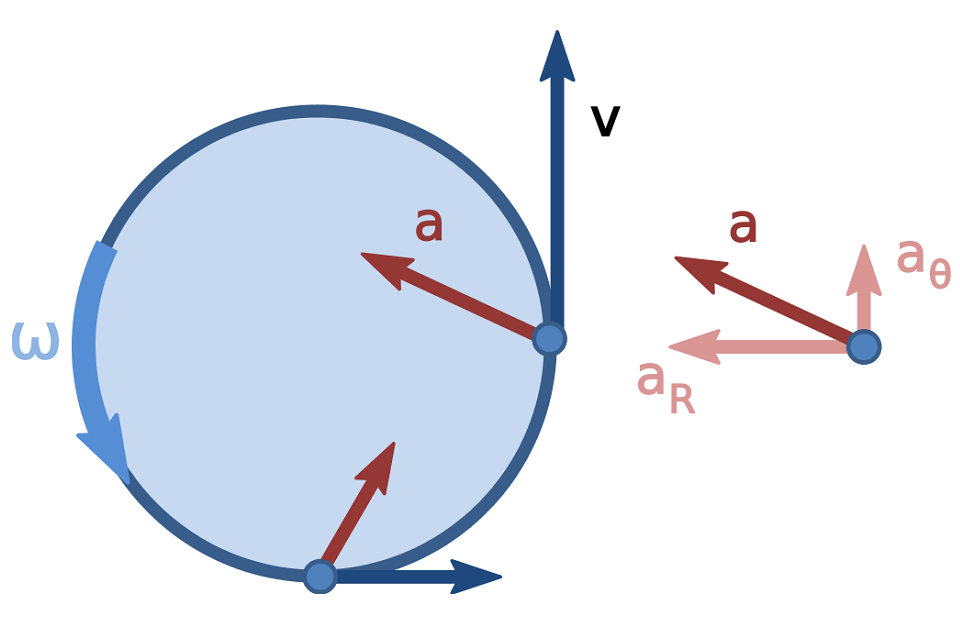
L’accélération (a) d’une particule est une grandeur vectorielle qui indique la vitesse à laquelle la vitesse change en fonction du temps; c’est-à-dire le changement du vecteur vitesse par unité de temps. L’accélération a généralement deux composantes: l’accélération tangentielle à la trajectoire et l’accélération qui lui est normale. L’accélération tangentielle est la cause de la variation du module de vitesse (célérité) par rapport au temps, alors que l’accélération normale est responsable du changement de direction de la vitesse. Les modules des deux composantes d’accélération dépendent de la distance entre la particule et l’axe de rotation.

Mouvement circulaire uniforme
Il se caractérise par une vitesse ou une constante structurelle variable, de sorte que l’accélération angulaire est nulle. La vitesse linéaire de la particule ne varie pas en module, mais en direction.L’accélération tangentielle est zéro; mais il y a une accélération centripète (accélération normale), qui est la cause du changement de direction.
Mathématiquement, la vitesse angulaire est exprimée par:

où  est la vitesse angulaire (constante),  est la variation de l’angle balayé par la particule et  C’est la variation du temps. L’angle parcouru dans un intervalle de temps est:

Mouvement circulaire uniformément accéléré
Dans ce mouvement, la vitesse angulaire varie linéairement avec le temps, le mobile étant soumis à une accélération angulaire constante. Les équations de mouvement sont analogues à celles du rectiligne uniformément accéléré, mais en utilisant des angles au lieu de distances: 

étant  , l’accélération angulaire constante.

Mouvement harmonique complexe
C’est un type de mouvement bidimensionnel ou tridimensionnel qui peut être construit comme une combinaison de simples mouvements harmoniques dans différentes directions. Lorsqu’une structure est soumise à des vibrations, le mouvement d’un point matériel particulier peut souvent être modélisé par un mouvement harmonique complexe si l’amplitude du mouvement est faible.

Le mouvement harmonique complexe est intéressant car ce n’est généralement pas un mouvement périodique, mais un mouvement quasi-périodique qui ne se répète jamais exactement, bien qu’il exécute presque des cycles sans se répéter exactement. La forme vectorielle d’un point qui exécute ce mouvement s’avère être:

où  ce sont les amplitudes maximales dans les trois directions de l’espace,  sont les fréquences d’oscillation et  les phases initiales (les conditions initiales permettent de calculer à la fois les amplitudes et les phases). Les fréquences dépendent des caractéristiques du système (masse, rigidité, etc.).

Le mouvement circulaire uniforme est en fait un cas de mouvement harmonique complexe dans lequel les amplitudes dans les deux directions sont égales au rayon du cercle.  , les fréquences dans les deux directions coïncident  et il y a une relation de lacunes spécifiques  . Si les amplitudes ne sont pas égales ou si le retard n’est pas exactement donné, la trajectoire de ce mouvement, mais les fréquences sont égales, le résultat est un mouvement elliptique.

Mouvement solide rigide
Tous les mouvements décrits ci-dessus se rapportent à des points matériels concrets, ou corpuscules, c’est-à-dire à des corps physiques dont les petites dimensions par rapport à la taille de la trajectoire permettent leur approximation par des points matériels. Cependant, les corps physiques macroscopiques ne sont pas ponctuels. Dans de nombreuses situations, le mouvement du corps dans son ensemble nécessite une description plus complexe que de supposer que tous ses points suivent une trajectoire beaucoup plus grande que les distances entre les points du corps, de sorte que la description du corps. le corps en tant que point matériel est inadéquat et la cinématique du point matériel est trop simple pour décrire correctement la cinématique du corps. Dans ces cas, il faut utiliser la cinématique du solide rigide, dans laquelle la « trajectoire » du corps se voit attribuer un espace plus complexe ou plus riche que le simple espace euclidien à trois dimensions, car il est nécessaire de définir non seulement le déplacement de le corps à travers ledit espace, mais de spécifier les changements d’orientation du corps dans son mouvement, au moyen de mouvements de rotation.

Formulation mathématique avec calcul différentiel
La vitesse est la dérivée temporelle du vecteur de position et l’accélération est la dérivée temporelle de la vitesse:

ou ses expressions intégrales:

où  ce sont les conditions initiales.

Mouvement sur terre
En observant le mouvement sur Terre de corps tels que des masses d’air en météorologie ou en projectiles, il y a des déviations causées par le soi-disant Effet Coriolis. Ils sont utilisés pour prouver que la Terre tourne sur son axe. Du point de vue cinématique, il est intéressant d’expliquer ce qui se passe lorsqu’on considère la trajectoire observée à partir d’un système de référence en rotation, la Terre.

Supposons qu’un canon à l’équateur lance un projectile vers le nord le long d’un méridien. Un observateur situé au nord sur le méridien observe que le projectile tombe à l’est de la chose prévue, s’écartant à droite de la trajectoire. De même, si le projectile avait tiré le long du méridien au sud, il aurait également dévié vers l’est, dans le cas présent à gauche de la trajectoire suivie. L’explication de cette « déviation », causée par l’effet Coriolis, est due à la rotation de la Terre. Le projectile a une vitesse à trois composantes: les deux affectant le tir parabolique, respectivement vers le nord (ou le sud) et vers le haut, plus une troisième composante perpendiculaire aux précédentes dues au projectile, avant de quitter le canyon, a une vitesse égale à la vitesse de rotation de la Terre à l’équateur. Cette dernière composante de la vitesse est la cause de la déviation observée car bien que la vitesse de rotation angulaire de la Terre soit constante sur toute sa surface, ce n’est pas la vitesse de rotation linéaire, qui est maximale à l’équateur et nulle au centre de la surface. les pôles.Ainsi, le projectile avance vers le nord (ou le sud), se déplace plus rapidement vers l’est que la surface de la Terre, de sorte que la déviation mentionnée est observée.

Un autre cas intéressant de mouvement sur Terre est celui du pendule de Foucault. Le plan d’oscillation du pendule ne reste pas fixe, mais nous l’observons en rotation, tournant dans le sens des aiguilles d’une montre dans l’hémisphère nord et dans le sens contraire des aiguilles d’une montre dans l’hémisphère sud. Si le pendule oscille à l’équateur, le plan d’oscillation ne change pas.Par contre, aux pôles, la rotation du plan d’oscillation prend une journée. Pour les latitudes intermédiaires, les valeurs les plus élevées dépendent de la latitude. L’explication d’un tel virage est basée sur les mêmes principes que ceux appliqués précédemment pour le projectile d’artillerie.

Cinématique relativiste
En relativité, ce qui est absolu est la vitesse de la lumière dans le vide, pas dans l’espace ou dans le temps. Chaque observateur dans un système de référence inertiel, quelle que soit sa vitesse relative, mesurera la même vitesse pour la lumière qu’un autre observateur dans un autre système.Ce n’est pas possible du point de vue classique. Les transformations de mouvement entre deux systèmes de référence doivent tenir compte de ce fait, à l’origine des transformations de Lorentz. Ils montrent que les dimensions spatiales et le temps sont liés, alors, en relativité, il est normal de parler d’espace-temps et d’un espace à quatre dimensions.

Il existe de nombreuses preuves expérimentales d’effets relativistes. Par exemple, le temps mesuré dans un laboratoire pour la désintégration d’une particule générée avec une vitesse proche de celle de la lumière est supérieur à la décroissance mesurée lorsque la particule est générée au repos par rapport au laboratoire. Ceci s’explique par la dilatation relativiste temporelle qui se produit dans le premier cas.

La cinématique est un cas particulier de géométrie différentielle de courbes, dans laquelle toutes les courbes sont paramétrées de la même manière: dans le temps. Pour le cas relativiste, le temps des coordonnées est une mesure relative pour chaque observateur; par conséquent, l’utilisation d’un certain type de mesure invariante est requise en tant qu’intervalle relativiste ou de manière équivalente pour les particules dont la masse est le temps propre. La relation entre le temps coordonné d’un observateur et le temps correct est donnée par le facteur de Lorentz.