La optimización de la topología (TO) es un método matemático que optimiza el diseño del material dentro de un espacio de diseño dado, para un conjunto dado de cargas, condiciones de contorno y restricciones con el objetivo de maximizar el rendimiento del sistema. TO es diferente de la optimización de la forma y la optimización del tamaño en el sentido de que el diseño puede alcanzar cualquier forma dentro del espacio de diseño, en lugar de tratar con configuraciones predefinidas.
La formulación convencional de TO utiliza un método de elementos finitos [FEM] para evaluar el desempeño del diseño. El diseño se optimiza utilizando técnicas de programación matemática basadas en gradientes, como el algoritmo de criterios de optimalidad y el método de mover asíntotas o algoritmos no basados en gradientes, como los algoritmos genéticos.
La optimización de topología tiene una amplia gama de aplicaciones en ingeniería aeroespacial, mecánica, bioquímica y civil. Actualmente, los ingenieros usan principalmente TO en el nivel de concepto de un proceso de diseño. Debido a las formas libres que ocurren naturalmente, el resultado es a menudo difícil de fabricar. Por esa razón, el resultado que surge de TO a menudo se ajusta para la fabricación. Agregar restricciones a la formulación para aumentar la capacidad de fabricación es un campo activo de investigación. En algunos casos, los resultados de TO se pueden fabricar directamente utilizando fabricación aditiva; Por lo tanto, TO es una parte clave del diseño para la fabricación aditiva.
Historia
Este método derivado de las matemáticas fue claramente definido, explicado y hecho utilizable para la mecánica en la década de 2000, en particular con el artículo fundador de Ole Sigmund.
El software de optimización topológica cada vez más sofisticado permite a los ingenieros guardar el material posible para un objeto mientras mantienen o mejoran su fuerza o flexibilidad (si es necesario) y teniendo en cuenta las restricciones que se colocarán en él. Anteriormente, se basa en la intuición, el método de prueba y error y / o el genio de los creadores y / o ingenieros de fabricación.
Un ejemplo muy simple es la reducción optimizada en el número de radios de una rueda de bicicleta. Hasta ahora solo se trataba de formas simples, porque estos softwares son muy codiciosos en el cálculo o se vieron limitados rápidamente por la complejidad del trabajo solicitado
En octubre de 2017, en la revista Nature, investigadores de una universidad danesa presentan un método para hacer este trabajo para objetos grandes, mejorando la resolución posible (una imagen 2d está compuesta de píxeles, mientras que una imagen 3D está compuesta de voxels. Hasta hace poco, el La resolución de los modelos 3D optimizados se limitó a 5 millones de voxels, pero un nuevo programa optimiza objetos de hasta 1 billón de voxels, lo que permite, por ejemplo, modelar y rediseñar optimizando un ala de Boeing 777 en un 5% mientras se refuerza desde el interior. por costillas curvas longitudinales y diagonales en lugar de en una cuadrícula … con un ahorro esperado de 200 toneladas de queroseno / año. Esto ha requerido días de cálculo por parte de una supercomputadora y este diseño (que evoca el interior de algunos huesos o partes internas de exoesqueletos de insectos) es actualmente «inmanejable», pero el progreso de la impresión 3D pronto podría ponerlo a nuestro alcance.
Planteamiento del problema
Un problema de optimización de topología se puede escribir en la forma general de un problema de optimización como:
La declaración del problema incluye lo siguiente:
Una funcion objetiva . Esta función representa la cantidad que se minimiza para un mejor rendimiento. La función objetivo más común es el cumplimiento, donde minimizar el cumplimiento lleva a maximizar la rigidez de una estructura.
La distribución del material como variable de problema. Esto se describe por la densidad del material en cada ubicación . El material está presente, indicado por un 1, o ausente, indicado por un 0.
El espacio de diseño . Esto indica el volumen permitido dentro del cual puede existir el diseño.Los requisitos de ensamblaje y embalaje, la accesibilidad humana y de herramientas son algunos de los factores que deben considerarse al identificar este espacio. Con la definición del espacio de diseño, las regiones o componentes en el modelo que no se pueden modificar durante el curso de la optimización se consideran regiones que no son de diseño.
restricciones Una característica que la solución debe satisfacer. Algunos ejemplos son la cantidad máxima de material a distribuir (restricción de volumen) o los valores de tensión máxima.
Metodologías de implementación
Existen varias metodologías de implementación que se han utilizado para resolver problemas de TO. En mecánica, resolver un problema de optimización topológica implica modelar la parte, o el conjunto de partes, para ser optimizado usando el método de elementos finitos. Un método clásico de optimización topológica consiste en considerar en cada punto del volumen de optimización una densidad de materia. que varía entre 0 y 1. Otros métodos consideran la orientación local del material (para materiales no isotrópicos) o incluso de otras características. En estos métodos, la optimización generalmente implica minimizar la energía de deformación de la estructura, lo que equivale a encontrar aproximadamente la estructura más rígida posible. Podemos establecer la cantidad de material utilizado para resaltar formas óptimas, para guiar un diseño y optimización realizado de otra manera, o buscar directamente definir una forma que minimice el material a implementar para minimizar la estructura máxima, respetando una restricción que no debe exceder.En la práctica, y los umbrales, en particular para imponer restricciones geométricas específicas relacionadas con el proceso de fabricación (simetrías, autorización de volumen hueco o no, …, plano de unión).
Los principales pasos y dificultades a superar son generalmente los siguientes:
Definir las especificaciones de la pieza a diseñar:
Espacio realmente disponible: a menudo es mucho más grande que la sala posiblemente existente, y se puede ampliar aún más al volver a colocar la función para completar y las restricciones que rodean esta sala, o el conjunto de salas para rediseñar. No debemos olvidar las áreas donde se impone o prohíbe el material (por razones funcionales o estéticas).
Conexiones mecánicas con el medio ambiente: es necesario poner a un lado las conexiones posibles con las partes vecinas, porque a menudo hay mucha más libertad para las zonas de amarres que las previstas a priori. A veces no está claro qué áreas bloquear o qué zonas se cargan por fuerzas, la más pragmática es imaginar cómo podría probarse la pieza en un banco de pruebas, con enlaces fijos y conectores, por ejemplo.
Fuerzas mecánicas sufridas: es necesario tener en cuenta todas las cargas mecánicas vistas por la parte, más allá de la función principal, es decir. esfuerzos relacionados con los pasos de fabricación (incluido el mecanizado), esfuerzos relacionados con el manejo de la pieza de trabajo (montaje / desmontaje de la pieza de trabajo, transporte), esfuerzos accidentales (choques), por ejemplo.
Simetrías y condiciones de fabricación (esto se tiene cada vez más en cuenta por los programas informáticos).
Inicie el cálculo de optimización topológica: la finura de la malla debe adaptarse a la precisión espacial deseada y a los recursos informáticos disponibles; Los cálculos pueden ser largos, por lo que tratamos de hacer los primeros cálculos en la escala de unos pocos minutos, luego los refinamos. También es necesario verificar cómo se tienen en cuenta los diferentes casos de carga por el algoritmo. De hecho, si uno solo busca la estructura más rígida posible para una masa dada, las energías de las diferentes cargas simplemente se suman, entonces es necesario ponderarlas, posiblemente. Por otro lado, si el objetivo es obtener la pieza más ligera posible que no se rompa, no hay necesidad de ponderación.
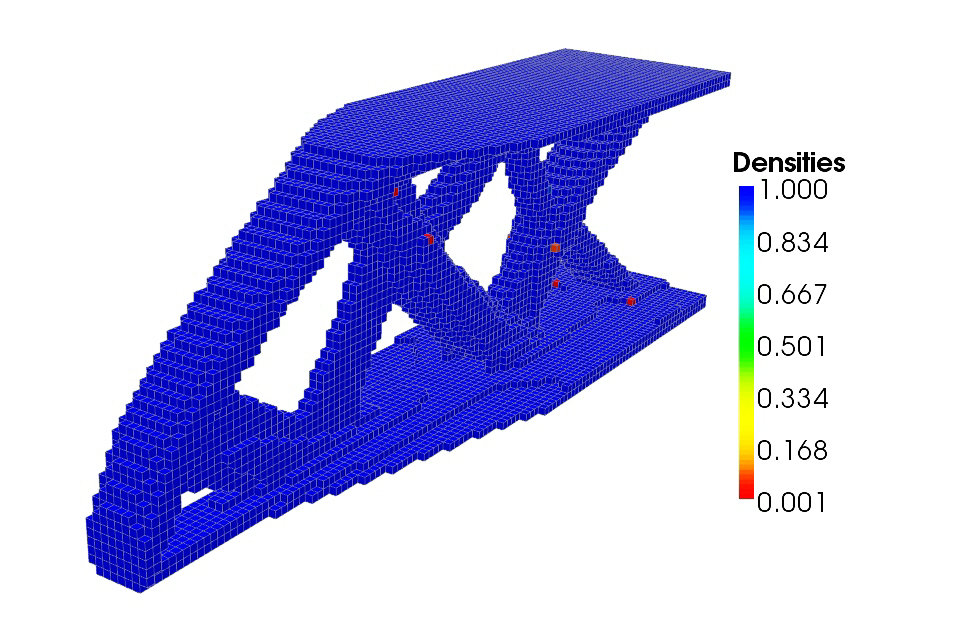
Análisis del resultado: para mostrar una parte fácilmente comprensible (con vacío y plenitud bien definidos), el software generalmente filtra el resultado para su visualización (por ejemplo, lleno corresponde a áreas de densidad de material superior al 50%, de lo contrario está vacío). Por lo tanto, es necesario tener en cuenta que, en general, se trata de una materia más o menos densa / porosa que realmente considera el algoritmo, y que las posibles zonas de materia no relacionadas con el resto son bastante posibles, al mismo tiempo. Mostrar, porque están vinculados al resto por material de baja densidad, no se muestra. El resultado es, por lo tanto, pretender definir una pieza hecha de vacío y llena, más cercana a lo que propone el algoritmo.
Existen parámetros (a veces ocultos) para explorar estas sutilezas en detalle: umbral del material (por defecto 50% en general), penalización (parámetro que limita las zonas de densidades alrededor del 50%, pero que puede degradar la convergencia de los algoritmos), filtrado / suavizado (filtro que permite eliminar detalles considerados demasiado pequeños) y, por supuesto, la finura de la malla (que permite revelar más o menos detalles finos). En esta etapa, a menudo se comprende que la forma obtenida es absurda, generalmente tras la omisión de una restricción importante, o porque el problema se planteó mal (por ejemplo, si no hay suficientes conexiones con el marco para mantener la habitación o porque los bloqueos o se han realizado esfuerzos en un área donde el material está prohibido). pero puede degradar la convergencia de los algoritmos), filtrando / suavizando (el filtro permite eliminar detalles considerados demasiado pequeños) y, por supuesto, la finura de la malla (lo que permite revelar más o menos detalles finos).
En esta etapa, a menudo se comprende que la forma obtenida es absurda, generalmente tras la omisión de una restricción importante, o porque el problema se planteó mal (por ejemplo, si no hay suficientes conexiones con el marco para mantener la habitación o porque los bloqueos o se han realizado esfuerzos en un área donde el material está prohibido). pero puede degradar la convergencia de los algoritmos), filtrando / suavizando (el filtro permite eliminar detalles considerados demasiado pequeños) y, por supuesto, la finura de la malla (lo que permite revelar más o menos detalles finos). En esta etapa, a menudo se comprende que la forma obtenida es absurda, generalmente tras la omisión de una restricción importante, o porque el problema se planteó mal (por ejemplo, si no hay suficientes conexiones con el marco para mantener la habitación o porque los bloqueos o se han realizado esfuerzos en un área donde el material está prohibido).
Dibujo y verificación: una vez que la interpretación de los resultados se consolida, la pieza se puede dibujar lo más cerca posible de la topología obtenida (número de barras / placas, orientación, grosores relativos), pero posiblemente más agradable a la vista, porque Las formas llamadas «orgánicas» obtenidas por optimización topológica no siempre son adecuadas. Esta es la razón por la que a veces imponemos una piel fuera de la habitación (la parte visible) limitando la optimización topológica solo dentro de la habitación a iluminar (parte invisible). Si es posible, es mejor usar celosías (es decir, una red estrecha de vigas o paredes, como espumas), para colocar material de densidad intermedia donde el cálculo lo haga aparecer (c ‘
Optimización de topología continua y discreta.
Se puede distinguir en optimización de topología continua y discreta. En la optimización de topología continua, se busca la distribución de material en el espacio de instalación. En la optimización de topología discreta, se buscan elementos discretos como cobertura del espacio de construcción. Por ejemplo, se puede buscar un marco óptimo, que en última instancia representa una topología del objeto general.
Optimización de topología continua
En la práctica, la optimización de topología se utiliza en el proceso de diseño para obtener propuestas para diseños iniciales de componentes. Al hacerlo, el diseñador debe determinar primero el espacio máximo disponible y las condiciones de contorno (cargas y restricciones). Estos datos se convierten en un modelo FE (FE = elementos finitos).
Básicamente, se hace una distinción según el material y la optimización de la topología geométrica.En la optimización de la topología geométrica, la geometría del componente se describe por la forma del límite exterior, es decir, los bordes y las superficies. Esto también se hacen recesos dentro del límite del componente y varían en forma. La optimización de la topología de materiales describe la geometría de una pieza en el espacio de diseño. Aquí, a cada elemento finito en el espacio de diseño se le asigna una densidad. Para algoritmos de optimización simples, como los criterios de optimalidad (por ejemplo, Diseño totalmente estresado), la densidad se establece en 0 o 100% como un simple interruptor de encendido / apagado. El diseño completamente estresado retiene los elementos que se encuentran cerca del esfuerzo máximo permitido, de modo que al final de la optimización casi todos los elementos de la malla FE se aprovechan al máximo en términos de resistencia. La programación matemática es un algoritmo de optimización que utiliza las derivadas parciales de la función objetivo para determinar el cambio de los parámetros individuales para la siguiente iteración. En consecuencia, debe haber una distribución de densidad continua para la diferenciabilidad. En el llamado método de homogeneización, el cambio de densidad se describe mediante un cuerpo hueco microscópico en cada uno de los elementos finitos y luego se transfiere a través de una ley de material macroscópico no lineal en un cambio en el módulo de elasticidad.Como resultado, se pueden calcular las tensiones y deformaciones del componente. Como resultado de dicha optimización de topología, obtiene un modelo de diseño robusto y poroso, que solo ofrece ayuda para encontrar una forma debido a la estructura similar a la de los huesos y al abandono de las restricciones de fabricación. Una forma de mejorar el resultado es devolver el modelo FE a un modelo de superficie de oneCAD suavizado. Si es necesario, también se pueden tener en cuenta las restricciones de fabricación.
Optimización de topología discreta
Una de las primeras optimizaciones de topología fue realizada por Anthony George Maldon Michell.Pero incluso hoy en día las optimizaciones de topología se llevan a cabo por armazones. La razón de esto es el bajo tiempo de cálculo; aunque la proximidad a la realidad es significativamente más remota que en el caso de la optimización de topología continua.
La resolución de problemas TO en un sentido discreto se realiza mediante la discretización del dominio de diseño en elementos finitos. Las densidades de material dentro de estos elementos se tratan como las variables de problema. En este caso, la densidad del material de uno indica la presencia de material, mientras que el cero indica una ausencia de material. Debido a que la complejidad topológica alcanzable del diseño depende de la cantidad de elementos, se prefiere una gran cantidad. Gran cantidad de elementos finitos aumenta la complejidad topológica alcanzable, pero tiene un costo. En primer lugar, resolver el sistema FEM se vuelve más costoso. En segundo lugar, los algoritmos que pueden manejar una gran cantidad (varios miles de elementos no es infrecuente) de variables discretas con múltiples restricciones no están disponibles. Además, son poco sensibles a las variaciones de los parámetros. En la literatura se han reportado problemas con hasta 30000 variables.
Resolviendo el problema con variables continuas.
Las complejidades indicadas anteriormente con la resolución de problemas TO mediante variables binarias han hecho que la comunidad busque otras opciones. Una de ellas es el modelado de las densidades con variables continuas. Las densidades de material ahora también pueden alcanzar valores entre cero y uno. Los algoritmos basados en gradientes que manejan grandes cantidades de variables continuas y múltiples restricciones están disponibles. Pero las propiedades del material tienen que ser modeladas en un entorno continuo. Esto se hace a través de la interpolación. Una de las metodologías de interpolación más implementadas es el método SIMP (material isotrópico sólido con penalización). Esta interpolación es esencialmente una ley de poder. . Interpola el módulo de Young del material al campo de selección escalar. El valor del parámetro de penalización. generalmente se toma entre . Se ha demostrado que esto confirma la microestructura de los materiales. En el método SIMP se agrega un límite inferior en el módulo de Young, , para asegurarse de que las derivadas de la función objetivo sean distintas de cero cuando la densidad sea cero. Cuanto más alto es el factor de penalización, más penaliza SIMP el algoritmo en el uso de densidades no binarias. Desafortunadamente, el parámetro de penalización también introduce no convexidades).
Formas derivadas
Derivados topologicos
Ajuste de nivel
Campo de fase
Optimización estructural evolutiva
Software comercial
Hay varios software de optimización de topología comercial en el mercado. La mayoría de ellos utiliza la optimización de topología como una sugerencia de cómo debe ser el diseño óptimo, y se requiere la reconstrucción manual de la geometría. Hay algunas soluciones que producen diseños óptimos listos para la fabricación aditiva.
Ejemplos
Cumplimiento estructural
Una estructura rígida es aquella que tiene el menor desplazamiento posible cuando se le da cierto conjunto de condiciones de contorno. Una medida global de los desplazamientos es la energía de tensión (también llamada cumplimiento) de la estructura bajo las condiciones de contorno prescritas.Cuanto menor es la energía de tensión, mayor es la rigidez de la estructura. Por lo tanto, la declaración del problema involucra el objetivo funcional de la energía de deformación que debe minimizarse.
En un nivel amplio, se puede visualizar que cuanto más material, menor será la deflexión, ya que habrá más material para resistir las cargas. Por lo tanto, la optimización requiere una restricción opuesta, la restricción de volumen. Esto es en realidad un factor de costo, ya que no queremos gastar mucho dinero en el material. Para obtener el material total utilizado, se puede realizar una integración del campo de selección sobre el volumen.
Finalmente, la elasticidad que gobierna las ecuaciones diferenciales se conecta para obtener la declaración final del problema.
sujeto a:
Pero, una implementación sencilla en el Marco de Elementos Finitos de tal problema es aún inviable debido a cuestiones como:
Dependencia de malla: la dependencia de malla significa que el diseño obtenido en una malla no es el que se obtendrá en otra malla. Las características del diseño se vuelven más complejas a medida que la malla se refina.
Inestabilidades numéricas: la selección de la región en forma de tablero de ajedrez.
Algunas técnicas, como el filtrado basado en el procesamiento de imágenes, se están utilizando actualmente para aliviar algunos de estos problemas.
La forma 3F3D sigue la fuerza de la impresión 3D
La proliferación actual de la tecnología de impresora 3D ha permitido a los diseñadores e ingenieros aprovechar las técnicas de optimización de topología al diseñar nuevos productos.
La optimización de topología combinada con la impresión en 3D permite un aligeramiento significativo, un mejor desempeño estructural y un ciclo de diseño a fabricación más corto.
Problemas multifísicos.
Interacción fluido-estructura
Termoelectricidad

 . Esta función representa la cantidad que se minimiza para un mejor rendimiento. La función objetivo más común es el cumplimiento, donde minimizar el cumplimiento lleva a maximizar la rigidez de una estructura.
. Esta función representa la cantidad que se minimiza para un mejor rendimiento. La función objetivo más común es el cumplimiento, donde minimizar el cumplimiento lleva a maximizar la rigidez de una estructura. . El material está presente, indicado por un 1, o ausente, indicado por un 0.
. El material está presente, indicado por un 1, o ausente, indicado por un 0. . Esto indica el volumen permitido dentro del cual puede existir el diseño.Los requisitos de ensamblaje y embalaje, la accesibilidad humana y de herramientas son algunos de los factores que deben considerarse al identificar este espacio. Con la definición del espacio de diseño, las regiones o componentes en el modelo que no se pueden modificar durante el curso de la optimización se consideran regiones que no son de diseño.
. Esto indica el volumen permitido dentro del cual puede existir el diseño.Los requisitos de ensamblaje y embalaje, la accesibilidad humana y de herramientas son algunos de los factores que deben considerarse al identificar este espacio. Con la definición del espacio de diseño, las regiones o componentes en el modelo que no se pueden modificar durante el curso de la optimización se consideran regiones que no son de diseño. restricciones
restricciones  Una característica que la solución debe satisfacer. Algunos ejemplos son la cantidad máxima de material a distribuir (restricción de volumen) o los valores de tensión máxima.
Una característica que la solución debe satisfacer. Algunos ejemplos son la cantidad máxima de material a distribuir (restricción de volumen) o los valores de tensión máxima. A menudo incluye resolver una ecuación diferencial. Esto se hace comúnmente usando el método de elementos finitos, ya que estas ecuaciones no tienen una solución analítica conocida.
A menudo incluye resolver una ecuación diferencial. Esto se hace comúnmente usando el método de elementos finitos, ya que estas ecuaciones no tienen una solución analítica conocida. . Interpola el módulo de Young del material al campo de selección escalar. El valor del parámetro de penalización.
. Interpola el módulo de Young del material al campo de selección escalar. El valor del parámetro de penalización.  generalmente se toma entre
generalmente se toma entre ![{\ displaystyle \ scriptstyle [1, \, 3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6b426658716615e9685915e67165f541ca73885) . Se ha demostrado que esto confirma la microestructura de los materiales. En el método SIMP se agrega un límite inferior en el módulo de Young,
. Se ha demostrado que esto confirma la microestructura de los materiales. En el método SIMP se agrega un límite inferior en el módulo de Young,  , para asegurarse de que las derivadas de la función objetivo sean distintas de cero cuando la densidad sea cero. Cuanto más alto es el factor de penalización, más penaliza SIMP el algoritmo en el uso de densidades no binarias. Desafortunadamente, el parámetro de penalización también introduce no convexidades).
, para asegurarse de que las derivadas de la función objetivo sean distintas de cero cuando la densidad sea cero. Cuanto más alto es el factor de penalización, más penaliza SIMP el algoritmo en el uso de densidades no binarias. Desafortunadamente, el parámetro de penalización también introduce no convexidades).
![\ scriptstyle \ rho \, \ in \, [0, \, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/77d91d86c0e856662098acc3e592f71ab5cdeae4)


