La teoría de las células solares explica el proceso mediante el cual la energía de la luz en los fotones se convierte en corriente eléctrica cuando los fotones chocan contra un dispositivo semiconductor adecuado. Los estudios teóricos son de uso práctico porque predicen los límites fundamentales de una célula solar y brindan orientación sobre los fenómenos que contribuyen a las pérdidas y la eficiencia de la célula solar.

Explicación simple
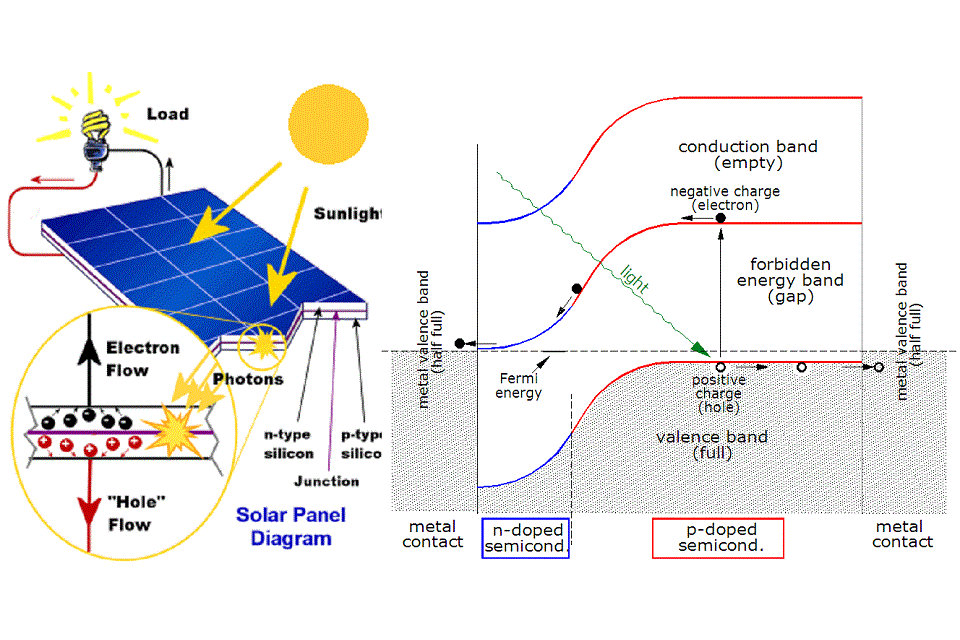
Los fotones a la luz del sol golpean el panel solar y son absorbidos por materiales semiconductores.

Los electrones (cargados negativamente) se desprenden de sus átomos cuando están excitados.Debido a su estructura especial y los materiales en las células solares, los electrones solo pueden moverse en una sola dirección. La estructura electrónica de los materiales es muy importante para que el proceso funcione, y a menudo el silicio que incorpora pequeñas cantidades de boro o fósforo se usa en diferentes capas.

Una serie de células solares convierte la energía solar en una cantidad utilizable de electricidad de corriente continua (CC).

Fotogeneración de portadores de carga
Cuando un fotón golpea una pieza de silicio, una de tres cosas puede suceder:
El fotón puede pasar directamente a través del silicio; esto (generalmente) ocurre para fotones de energía más baja.

El fotón puede reflejarse en la superficie.
El fotón puede ser absorbido por el silicio si la energía del fotón es mayor que el valor de la banda de silicio. Esto genera un par de electrón-agujero y a veces calor dependiendo de la estructura de la banda.

Cuando un fotón se absorbe, su energía se le da a un electrón en la red cristalina. Por lo general, este electrón está en la banda de valencia. La energía que el fotón le da al electrón la «excita» dentro de la banda de conducción, donde es libre para moverse dentro del semiconductor. La red de enlaces covalentes de la que anteriormente formaba parte el electrón ahora tiene un electrón menos. Esto se conoce como un hoyo. La presencia de un enlace covalente que falta permite que los electrones enlazados de los átomos vecinos se muevan hacia el «agujero», dejando otro agujero atrás, propagando agujeros a través de la red. Se puede decir que los fotones absorbidos en el semiconductor crean pares de electrón-agujero.

Un fotón solo necesita tener una energía mayor que la del espacio de banda para excitar un electrón de la banda de valencia a la banda de conducción. Sin embargo, el espectro de frecuencia solar se aproxima a un espectro de cuerpo negro a aproximadamente 5.800 K, y como tal, gran parte de la radiación solar que llega a la Tierra está compuesta de fotones con energías superiores a la banda de silicio. Estos fotones de mayor energía serán absorbidos por la célula solar, pero la diferencia de energía entre estos fotones y la brecha de banda de silicio se convierte en calor (a través de vibraciones reticulares llamadas fonones) en lugar de en energía eléctrica utilizable. El efecto fotovoltaico también puede ocurrir cuando dos fotones se absorben simultáneamente en un proceso llamado efecto fotovoltaico de dos fotones. Sin embargo, se requieren altas intensidades ópticas para este proceso no lineal.

La unión pn
La célula solar más conocida se configura como una unión pn de área extensa hecha de silicio.Como simplificación, uno puede imaginar poner una capa de silicio de tipo n en contacto directo con una capa de silicio de tipo p. En la práctica, las uniones pn de las células solares de silicio no se hacen de esta manera, sino más bien mediante la difusión de un dopante de tipo n en un lado de una oblea de tipo p (o viceversa).

Si una pieza de silicio de tipo p se coloca en contacto cercano con una pieza de silicio de tipo n, se produce una difusión de electrones desde la región de alta concentración de electrones (el lado de tipo n de la unión) a la región de baja concentración de electrones (lado tipo p de la unión). Cuando los electrones se difunden a través de la unión pn, se recombinan con agujeros en el lado tipo p. Sin embargo (en ausencia de un circuito externo) esta difusión de portadoras no se prolonga indefinidamente porque las cargas se acumulan a cada lado de la unión y crean un campo eléctrico.El campo eléctrico promueve el flujo de carga, conocido como corriente de deriva, que se opone y finalmente equilibra la difusión de electrones y agujeros. Esta región donde los electrones y los agujeros se han difundido a través de la unión se llama región de agotamiento porque prácticamente no contiene portadores de carga móvil. También se conoce como la región de carga espacial, aunque la carga espacial se extiende un poco más en ambas direcciones que la región de agotamiento.

Separación del transportador de carga
Hay dos causas de movimiento y separación del portador de carga en una célula solar:
deriva de portadores, impulsados ​​por el campo eléctrico, con electrones que se empujan hacia un lado y agujeros hacia el otro lado

difusión de portadores desde zonas de mayor concentración de portador a zonas de menor concentración de portador (siguiendo un gradiente de potencial electroquímico).

Estas dos «fuerzas» pueden funcionar una contra la otra en cualquier punto dado de la celda. Por ejemplo, un electrón que se mueve a través de la unión de la región p a la región n (como en el diagrama al principio de este artículo) está siendo empujado por el campo eléctrico contra el gradiente de concentración. Lo mismo ocurre con un agujero que se mueve en la dirección opuesta.

Es más fácil entender cómo se genera una corriente al considerar pares de electrón-agujero que se crean en la zona de agotamiento, que es donde hay un campo eléctrico fuerte. El electrón es empujado por este campo hacia el lado n y el agujero hacia el lado p. (Esto es opuesto a la dirección de la corriente en un diodo polarizado, como un diodo emisor de luz en funcionamiento.) Cuando el par se crea fuera de la zona de carga espacial, donde el campo eléctrico es más pequeño, la difusión también actúa para moverse los portadores, pero la unión todavía juega un rol al barrer los electrones que lo alcanzan desde el lado p al lado n, y al barrer cualquier orificio que lo alcance desde el lado n al lado p, creando así un gradiente de concentración fuera del zona de carga espacial

En las celdas solares gruesas hay muy poco campo eléctrico en la región activa fuera de la zona de carga espacial, por lo que el modo dominante de separación del transportador de carga es la difusión. En estas células, la longitud de difusión de los portadores minoritarios (la longitud que los portadores fotogenerados pueden viajar antes de recombinarse) debe ser grande en comparación con el grosor de la célula. En las células de película delgada (como el silicio amorfo), la longitud de difusión de los portadores minoritarios suele ser muy corta debido a la existencia de defectos, y la separación de carga dominante es por lo tanto deriva, impulsada por el campo electrostático de la unión, que se extiende al todo el espesor de la celda.

Una vez que el operador minoritario ingresa a la región de deriva, se ‘barre’ a través del cruce y, en el otro lado del cruce, se convierte en un transportista mayoritario. Esta corriente inversa es una corriente de generación, alimentada tanto térmicamente como (si está presente) por la absorción de la luz. Por otro lado, los portadores mayoritarios son conducidos a la región de deriva por difusión (como resultado del gradiente de concentración), que conduce a la corriente directa; solo la mayoría de los portadores con las energías más altas (en la llamada cola de Boltzmann, véase la estadística de Maxwell-Boltzmann) pueden cruzar completamente la región de deriva. Por lo tanto, la distribución de portadora en todo el dispositivo está gobernada por un equilibrio dinámico entre la corriente inversa y la corriente directa.

Conexión a una carga externa
Los contactos semiconductores de metal óhmico se fabrican para los lados de tipo ny de tipo p de la célula solar, y los electrodos se conectan a una carga externa. Los electrones que se crean en el lado tipo n, o se crean en el lado tipo p, «recogidos» por la unión y barridos en el lado tipo n, pueden viajar a través del cable, alimentar la carga y continuar a través del cable hasta que lleguen al contacto semiconductor-metal de tipo p. Aquí, se recombinan con un agujero que se creó como un par de electrón-agujero en el lado de tipo p de la célula solar, o un agujero que se barrió a través de la unión desde el lado de tipo n después de haber sido creado allí.

El voltaje medido es igual a la diferencia en los niveles cuasi de Fermi de los portadores mayoritarios (electrones en la porción de tipo ny agujeros en la porción de tipo p) en los dos terminales.

Circuito equivalente de una célula solar
Para comprender el comportamiento electrónico de una célula solar, es útil crear un modelo que sea eléctricamente equivalente, y se base en componentes eléctricos ideales discretos cuyo comportamiento esté bien definido. Una célula solar ideal puede ser modelada por una fuente de corriente en paralelo con un diodo; en la práctica, ninguna célula solar es ideal, por lo que se añaden al modelo una resistencia de derivación y un componente de resistencia en serie. El circuito equivalente resultante de una celda solar se muestra a la izquierda. También se muestra, a la derecha, la representación esquemática de una célula solar para su uso en diagramas de circuitos.

Ecuación característica
Del circuito equivalente es evidente que la corriente producida por la célula solar es igual a la producida por la fuente de corriente, menos la que fluye a través del diodo, menos la que fluye a través de la resistencia en derivación:

dónde
I = corriente de salida (amperio)
I _L = corriente fotogenerada (amperios)
I _D = corriente de diodo (amperio)
I _SH = corriente de derivación (amperio).

La corriente a través de estos elementos se rige por el voltaje en ellos:

dónde
V _j = tensión en ambos diodos y resistencia RSH (voltios)
V = tensión en los terminales de salida (voltios)
I = corriente de salida (amperio)
R _S = resistencia en serie (Ω).

Según la ecuación del diodo de Shockley, la corriente desviada a través del diodo es:

dónde
I ₀ = corriente de saturación inversa (amperios)
n = factor de idealidad del diodo (1 para un diodo ideal)
q = carga elemental
k = Constante de Boltzmann
T = temperatura absoluta

 la tensión térmica. A 25 ° C,  voltio.
Según la ley de Ohm, la corriente desviada a través de la resistencia shunt es:

dónde
R _SH = resistencia de derivación (Ω).

Sustituirlos en la primera ecuación produce la ecuación característica de una célula solar, que relaciona los parámetros de la célula solar con la corriente y el voltaje de salida:

Una derivación alternativa produce una ecuación similar en apariencia, pero con V en el lado izquierdo. Las dos alternativas son identidades; es decir, producen precisamente los mismos resultados.

Dado que los parámetros I ₀ , n, R _S y R _SH no se pueden medir directamente, la aplicación más común de la ecuación característica es la regresión no lineal para extraer los valores de estos parámetros sobre la base de su efecto combinado sobre el comportamiento de la célula solar.

Cuando R _S no es cero, la ecuación anterior no da la corriente I directamente, pero puede resolverse usando la función de Lambert W:

Cuando se usa una carga externa con la celda, su resistencia simplemente puede agregarse a RS y V a cero para encontrar la corriente.

Cuando R _SH es infinito hay una solución para V para cualquier  menos que  :

De lo contrario, uno puede resolver para V usando la función de Lambert W:

Sin embargo, cuando R _SH es grande, es mejor resolver numéricamente la ecuación original.
La forma general de la solución es una curva con I disminuyendo a medida que V aumenta. La pendiente en V pequeña o negativa (donde la función W está cerca de cero) se acerca  , mientras que la pendiente a alta V se acerca  .

Voltaje de circuito abierto y corriente de cortocircuito
Cuando la celda se opera en circuito abierto, I = 0 y la tensión en los terminales de salida se define como la tensión de circuito abierto . Suponiendo que la resistencia de derivación es lo suficientemente alta como para descuidar el término final de la ecuación característica, el voltaje de circuito abierto V _OC es:

De manera similar, cuando la celda se opera en cortocircuito, V = 0 y la corriente I a través de los terminales se define como la corriente de cortocircuito. Se puede demostrar que para una celda solar de alta calidad (bajo R _S e I ₀ , y alta R _SH ) la corriente de cortocircuito I _SC es:

No es posible extraer energía del dispositivo cuando se opera ya sea en circuito abierto o en condiciones de cortocircuito.

Efecto del tamaño físico
Los valores de IL, I0, RS y RSH dependen del tamaño físico de la célula solar. Al comparar células por lo demás idénticas, una celda con el doble del área de unión de otra tendrá, en principio, el doble de IL e I0 porque tiene el doble del área donde se genera la fotocorriente y a través de la cual puede fluir la corriente del diodo. Por el mismo argumento, también tendrá la mitad de RS de la resistencia de la serie relacionada con el flujo de corriente vertical; sin embargo, para las células solares de silicio de gran área, la escala de la resistencia en serie encontrada por el flujo de corriente lateral no es fácilmente predecible ya que dependerá fundamentalmente del diseño de la rejilla (no está claro qué significa «por lo demás idéntico» a este respecto). Dependiendo del tipo de derivación, la celda más grande también puede tener la mitad de la RSH porque tiene el doble del área donde pueden ocurrir las derivaciones; por otro lado, si las derivaciones ocurren principalmente en el perímetro, entonces la RSH disminuirá de acuerdo con el cambio en la circunferencia, no en el área.

Como los cambios en las corrientes son los dominantes y se equilibran entre sí, la tensión de circuito abierto es prácticamente la misma; VOC comienza a depender del tamaño de la celda solo si la RSH es demasiado baja. Para tener en cuenta el predominio de las corrientes, la ecuación característica se escribe frecuentemente en términos de densidad de corriente o corriente producida por área de celda unitaria:

dónde
J = densidad de corriente (amperio / cm ² )
J _L = densidad de corriente fotogenerada (amperio / cm ² )
J ₀ = densidad de corriente de saturación inversa (amperios / cm ² )
r _S = resistencia de serie específica (Ω-cm ² )
r _SH = resistencia de derivación específica (Ω-cm ² ).

Esta formulación tiene varias ventajas. Una es que dado que las características de las celdas están referenciadas a un área común de sección transversal, pueden compararse para celdas de diferentes dimensiones físicas. Si bien esto tiene un beneficio limitado en un entorno de fabricación, donde todas las células tienden a tener el mismo tamaño, es útil en la investigación y en la comparación de células entre fabricantes. Otra ventaja es que la ecuación de densidad escala naturalmente los valores de los parámetros a órdenes de magnitud similares, lo que puede hacer que la extracción numérica de los mismos sea más simple y más precisa incluso con métodos de solución ingenuos.

Hay limitaciones prácticas de esta formulación. Por ejemplo, ciertos efectos parasitarios cobran importancia a medida que el tamaño de las células se reduce y puede afectar los valores de los parámetros extraídos. La recombinación y la contaminación de la unión tienden a ser mayores en el perímetro de la célula, por lo que las células muy pequeñas pueden exhibir valores más altos de J0 o valores más bajos de RSH que las células más grandes que son por lo demás idénticas. En tales casos, las comparaciones entre células deben realizarse con cautela y teniendo en cuenta estos efectos.
Este enfoque solo debe usarse para comparar celdas solares con un diseño comparable. Por ejemplo, una comparación entre células solares principalmente cuadráticas como células solares de silicio cristalino típicas y células solares estrechas pero largas como células solares de película delgada típicas puede conducir a suposiciones erróneas causadas por los diferentes tipos de rutas de corriente y por lo tanto la influencia de, por ejemplo, una contribución de resistencia de serie distribuida a rS. La macroarquitectura de las células solares podría ocasionar que se coloquen diferentes áreas de superficie en cualquier volumen fijo, particularmente para células solares de película delgada y células solares flexibles que pueden permitir estructuras plegadas altamente intrincadas. Si el volumen es la restricción de enlace, entonces la densidad de eficiencia basada en el área de superficie puede ser menos relevante.

Electrodos conductores transparentes
Los electrodos conductores transparentes son componentes esenciales de las células solares. Es una película continua de óxido de indio y estaño o una red de cables conductores, en la que los cables son colectores de carga, mientras que los huecos entre los cables son transparentes para la luz. Una densidad óptima de red de cables es esencial para el máximo rendimiento de la célula solar ya que una mayor densidad de cables bloquea la transmitancia de la luz, mientras que una menor densidad conduce a grandes pérdidas de recombinación debido a la mayor distancia recorrida por los portadores de carga.

Temperatura de la celda
La temperatura afecta la ecuación característica de dos maneras: directamente, a través de T en el término exponencial, e indirectamente a través de su efecto en I0 (estrictamente hablando, la temperatura afecta a todos los términos, pero estos dos mucho más significativamente que los demás). Mientras que aumentar T reduce la magnitud del exponente en la ecuación característica, el valor de I0 aumenta exponencialmente con T. El efecto neto es reducir VOC (voltaje de circuito abierto) linealmente con el aumento de la temperatura. La magnitud de esta reducción es inversamente proporcional a VOC; es decir, las celdas con valores más altos de VOC sufren reducciones más pequeñas de voltaje al aumentar la temperatura. Para la mayoría de las células solares de silicio cristalino, el cambio en COV con temperatura es de aproximadamente -0.50% / ° C, aunque la tasa para las células de silicio cristalino de mayor eficiencia es de alrededor de -0.35% / ° C. A modo de comparación, la tasa de células solares de silicio amorfo es de -0.20% / ° C a -0.30% / ° C, dependiendo de cómo se fabrique la célula.

La cantidad de corriente fotogenerada IL aumenta ligeramente al aumentar la temperatura debido a un aumento en el número de portadores generados térmicamente en la célula. Sin embargo, este efecto es leve: aproximadamente 0,065% / ° C para las células de silicio cristalino y 0,09% para las células de silicio amorfo.

El efecto general de la temperatura en la eficiencia de la celda se puede calcular utilizando estos factores en combinación con la ecuación característica. Sin embargo, dado que el cambio de voltaje es mucho más fuerte que el cambio en la corriente, el efecto general sobre la eficiencia tiende a ser similar al del voltaje. La mayoría de las células solares de silicio cristalino disminuyen en eficiencia en 0.50% / ° C y la mayoría de las células amorfas disminuyen en 0.15-0.25% / ° C. La figura anterior muestra curvas IV que se pueden ver típicamente para una célula solar de silicio cristalino a diversas temperaturas.

Resistencia en serie
A medida que aumenta la resistencia en serie, la caída de tensión entre la tensión de unión y la tensión del terminal aumenta para la misma corriente. El resultado es que la porción controlada por la corriente de la curva IV comienza a combarse hacia el origen, produciendo una disminución significativa en la tensión del terminal.  y una ligera reducción de ISC, la corriente de cortocircuito. Valores muy altos de RS también producirán una reducción significativa en ISC; en estos regímenes, domina la resistencia en serie y el comportamiento de la célula solar se asemeja al de una resistencia. Estos efectos se muestran para las células solares de silicio cristalino en las curvas IV que se muestran en la figura de la derecha.

Las pérdidas causadas por la resistencia en serie están en una primera aproximación dada por P_loss = V _Rs I = I ² R _S y aumentan cuadráticamente con la corriente (foto). Por lo tanto, las pérdidas de resistencia en serie son más importantes a altas intensidades de iluminación.

Resistencia shunt
A medida que disminuye la resistencia de derivación, la corriente desviada a través de la resistencia de derivación aumenta para un nivel dado de voltaje de unión. El resultado es que la porción controlada por voltaje de la curva IV comienza a ceder lejos del origen, produciendo una disminución significativa en la corriente I terminal y una ligera reducción en VOC. Los valores muy bajos de RSH producirán una reducción significativa en VOC. Al igual que en el caso de una resistencia de serie alta, una célula solar mal derivada asumirá características de funcionamiento similares a las de una resistencia. Estos efectos se muestran para las células solares de silicio cristalino en las curvas IV que se muestran en la figura de la derecha.

Corriente de saturación inversa
Si uno asume resistencia infinita de derivación, la ecuación característica se puede resolver para V_OC :

Por lo tanto, un aumento en I0 produce una reducción en COV proporcional al inverso del logaritmo del aumento. Esto explica matemáticamente el motivo de la reducción de VOC que acompaña a los aumentos de temperatura descritos anteriormente. El efecto de la corriente de saturación inversa en la curva IV de una célula solar de silicio cristalino se muestra en la figura de la derecha.Físicamente, la corriente de saturación inversa es una medida de la «fuga» de portadores a través de la unión pn en polarización inversa. Esta fuga es el resultado de la recombinación del portador en las regiones neutrales a ambos lados de la unión.

Factor de la ideología
El factor de idealidad (también llamado factor de emisividad) es un parámetro apropiado que describe cuán estrechamente el comportamiento del diodo coincide con el predicho por la teoría, que supone que la unión pn del diodo es un plano infinito y no se produce recombinación dentro de la región de carga espacial. Una coincidencia perfecta con la teoría se indica cuando n = 1. Cuando la recombinación en la región de carga espacial domina otra recombinación, sin embargo, n = 2. El efecto de cambiar el factor de idealidad independientemente de todos los demás parámetros se muestra para una célula solar de silicio cristalino en las curvas IV que se muestran en la figura a la derecha.

La mayoría de las células solares, que son bastante grandes en comparación con los diodos convencionales, se aproximan bastante a un plano infinito y generalmente exhibirán un comportamiento casi ideal bajo la Condición de prueba estándar (n ≈ 1). Bajo ciertas condiciones de operación, sin embargo, la operación del dispositivo puede estar dominada por la recombinación en la región de carga espacial. Esto se caracteriza por un aumento significativo en I0 así como un aumento en el factor de idealidad a n ≈ 2. Este último tiende a aumentar el voltaje de salida de la célula solar mientras que el primero actúa para erosionarlo. El efecto neto, por lo tanto, es una combinación del aumento de voltaje que se muestra para aumentar n en la figura a la derecha y la disminución de voltaje que se muestra para aumentar I0 en la figura anterior. Típicamente, I0 es el factor más significativo y el resultado es una reducción en el voltaje.

A veces, se observa que el factor de idealidad es mayor que 2, lo que generalmente se atribuye a la presencia de diodo Schottky o heterounión en la célula solar. La presencia de un desplazamiento de heterounión reduce la eficiencia de recolección de la célula solar y puede contribuir al bajo factor de llenado.