Die Theorie der Solarzellen erklärt den Vorgang, bei dem Lichtenergie in Photonen in elektrischen Strom umgewandelt wird, wenn die Photonen auf ein geeignetes Halbleiterbauelement treffen. Die theoretischen Studien sind von praktischem Nutzen, da sie die fundamentalen Grenzen einer Solarzelle vorhersagen und Hinweise zu den Phänomenen liefern, die zu Verlusten und Solarzelleneffizienz beitragen.

Einfache Erklärung
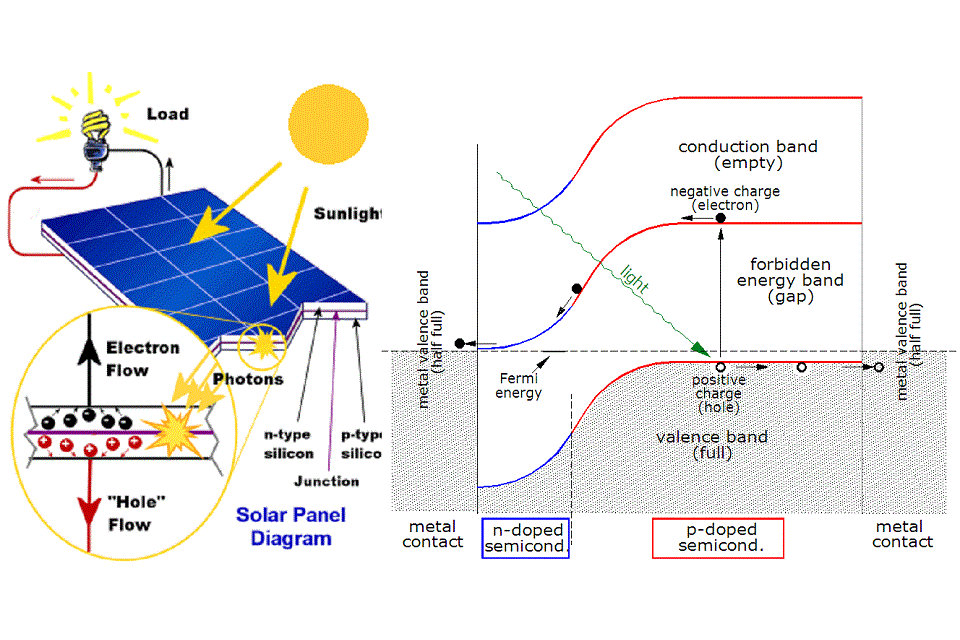
Photonen im Sonnenlicht treffen auf das Solarpanel und werden von halbleitenden Materialien absorbiert.

Elektronen (negativ geladen) werden von ihren Atomen gelöst, wenn sie angeregt werden. Aufgrund ihrer speziellen Struktur und der Materialien in Solarzellen dürfen sich die Elektronen nur in einer Richtung bewegen. Die elektronische Struktur der Materialien ist sehr wichtig für den Prozess zu arbeiten, und oft Silizium mit geringen Mengen von Bor oder Phosphor in verschiedenen Schichten verwendet wird.

Eine Reihe von Solarzellen wandelt Solarenergie in eine nutzbare Menge Gleichstrom (DC) um.

Photogeneration von Ladungsträgern
Wenn ein Photon auf ein Stück Silizium trifft, kann eines von drei Dingen passieren:
Das Photon kann direkt durch das Silizium gehen – dies geschieht (im Allgemeinen) für Photonen mit niedrigerer Energie.

Das Photon kann von der Oberfläche reflektiert werden.
Das Photon kann von dem Silizium absorbiert werden, wenn die Photonenenergie höher als der Siliziumbandlückenwert ist. Dies erzeugt ein Elektron-Loch-Paar und erhitzt sich manchmal in Abhängigkeit von der Bandstruktur.

Wenn ein Photon absorbiert wird, wird seine Energie einem Elektron im Kristallgitter gegeben.Normalerweise befindet sich dieses Elektron im Valenzband. Die Energie, die dem Elektron durch das Photon gegeben wird, „erregt“ es in das Leitungsband, wo es sich frei innerhalb des Halbleiters bewegen kann. Das Netzwerk kovalenter Bindungen, an dem das Elektron früher beteiligt war, hat jetzt ein Elektron weniger. Dies ist bekannt als ein Loch. Das Vorhandensein einer fehlenden kovalenten Bindung ermöglicht es den gebundenen Elektronen benachbarter Atome, sich in das „Loch“ zu bewegen, wobei ein weiteres Loch zurückgelassen wird, wodurch sich Löcher im gesamten Gitter ausbreiten. Man kann sagen, dass im Halbleiter absorbierte Photonen Elektron-Loch-Paare erzeugen.

Ein Photon muss nur eine Energie haben, die größer ist als die der Bandlücke, um ein Elektron vom Valenzband in das Leitungsband anzuregen. Das Solarfrequenzspektrum nähert sich jedoch einem Schwarzkörperspektrum bei etwa 5.800 K, und daher besteht ein Großteil der Sonnenstrahlung, die die Erde erreicht, aus Photonen mit Energien, die größer sind als die Bandlücke von Silizium. Diese Photonen höherer Energie werden von der Solarzelle absorbiert, aber der Energieunterschied zwischen diesen Photonen und der Siliziumbandlücke wird in Wärme umgewandelt (über Gitterschwingungen – Phononen genannt) und nicht in nutzbare elektrische Energie. Der photovoltaische Effekt kann auch auftreten, wenn zwei Photonen gleichzeitig in einem als Zweiphotonenphotovoltaik-Effekt bezeichneten Prozess absorbiert werden. Für diesen nichtlinearen Prozess sind jedoch hohe optische Intensitäten erforderlich.

Die PN-Kreuzung
Die bekannteste Solarzelle ist als großflächiger pn-Übergang aus Silizium ausgeführt. Als eine Vereinfachung kann man sich vorstellen, eine Siliziumschicht vom n-Typ in direkten Kontakt mit einer Siliziumschicht vom p-Typ zu bringen. In der Praxis werden pn-Übergänge von Siliziumsolarzellen nicht auf diese Weise hergestellt, sondern durch Diffusion eines n-Dotierstoffs in eine Seite eines p-Typ-Wafers (oder umgekehrt).

Wenn ein Stück Silizium vom p-Typ in engem Kontakt mit einem Stück Silizium vom n-Typ angeordnet wird, dann tritt eine Diffusion von Elektronen von dem Bereich hoher Elektronenkonzentration (die Seite vom n-Typ der Verbindung) in den Bereich von Niedrig auf Elektronenkonzentration (p-Typ Seite der Verbindung). Wenn die Elektronen über den pn-Übergang diffundieren, rekombinieren sie mit Löchern auf der p-Typ-Seite. Jedoch (in Abwesenheit einer externen Schaltung) geht diese Diffusion der Ladungsträger nicht unbegrenzt weiter, da sich Ladungen auf beiden Seiten der Verbindung aufbauen und ein elektrisches Feld erzeugen. Das elektrische Feld fördert den Ladungsfluss, bekannt als Driftstrom, der die Diffusion von Elektronen und Löchern entgegenwirkt und schließlich ausgleicht. Diese Region, in der Elektronen und Löcher über die Verbindung diffundiert sind, wird als Verarmungsregion bezeichnet, da sie praktisch keine mobilen Ladungsträger enthält. Es ist auch als die Raumladungszone bekannt, obwohl sich die Raumladung in beiden Richtungen etwas weiter erstreckt als die Verarmungszone.

Ladungsträgertrennung
Es gibt zwei Ursachen für die Bewegung und Trennung von Ladungsträgern in einer Solarzelle:
Drift von Trägern, angetrieben durch das elektrische Feld, wobei Elektronen in eine Richtung gedrückt werden und Löcher in die andere Richtung

Diffusion von Trägern von Zonen mit höherer Trägerkonzentration zu Zonen mit geringerer Trägerkonzentration (nach einem Gradienten des elektrochemischen Potentials).

Diese beiden „Kräfte“ können an jedem beliebigen Punkt in der Zelle gegeneinander wirken. Zum Beispiel wird ein Elektron, das sich durch die Verbindung von der p-Region zur n-Region bewegt (wie in dem Diagramm zu Beginn dieses Artikels), durch das elektrische Feld gegen den Konzentrationsgradienten gedrückt. Dasselbe gilt für ein Loch, das sich in die entgegengesetzte Richtung bewegt.

Es ist am einfachsten zu verstehen, wie ein Strom erzeugt wird, wenn Elektron-Loch-Paare betrachtet werden, die in der Verarmungszone erzeugt werden, in der sich ein starkes elektrisches Feld befindet. Das Elektron wird von diesem Feld zur Seite n und zum Loch zur Seite p geschoben.(Dies ist entgegengesetzt zu der Richtung des Stroms in einer in Durchlassrichtung vorgespannten Diode, wie beispielsweise einer lichtemittierenden Diode im Betrieb.) Wenn das Paar außerhalb der Raumladungszone erzeugt wird, wo das elektrische Feld kleiner ist, wirkt auch die Diffusion die Ladungsträger, aber die Verbindung spielt immer noch eine Rolle, indem sie alle Elektronen, die von der p – zur n – Seite gelangen, überstreicht und alle Löcher, die sie von der n – zur p – Seite erreichen, überstreicht und dadurch einen Konzentrationsgradienten außerhalb der Raumladungszone.

In dicken Solarzellen gibt es sehr wenig elektrisches Feld im aktiven Bereich außerhalb der Raumladungszone, so dass die dominierende Art der Ladungsträgertrennung die Diffusion ist. In diesen Zellen muss die Diffusionslänge von Minoritätsträgern (die Länge, die photogenerierte Träger durchlaufen können, bevor sie rekombinieren) im Vergleich zur Zellendicke groß sein. In Dünnschichtzellen (wie beispielsweise amorphem Silizium) ist die Diffusionslänge von Minoritätsträgern aufgrund der Existenz von Defekten üblicherweise sehr kurz und die dominierende Ladungstrennung ist daher eine Drift, die durch das elektrostatische Feld der Verbindung, das sich bis zu den Grenzflächen erstreckt, angetrieben wird ganze Dicke der Zelle.

Sobald der Minoritätsträger in die Driftregion eintritt, wird er über die Verbindungsstelle „gewobbelt“ und auf der anderen Seite der Verbindungsstelle zu einem Mehrheitsträger. Dieser Rückstrom ist ein Erzeugungsstrom, der sowohl thermisch als auch (falls vorhanden) durch die Absorption von Licht gespeist wird. Auf der anderen Seite werden Majoritätsladungsträger durch Diffusion (resultierend aus dem Konzentrationsgradienten) in die Drift-Region getrieben, was zu dem Vorwärtsstrom führt;nur die Majoritätsträger mit den höchsten Energien (im sogenannten Boltzmann-Tail; vgl. Maxwell-Boltzmann-Statistik) können die Drift-Region vollständig durchqueren. Daher wird die Trägerverteilung in der gesamten Vorrichtung durch ein dynamisches Gleichgewicht zwischen Rückstrom und Vorwärtsstrom bestimmt.

Verbindung zu einer externen Last
Ohmsche Metall-Halbleiter-Kontakte werden sowohl auf der n-Typ- als auch auf der p-Typ-Seite der Solarzelle hergestellt, und die Elektroden werden mit einer externen Last verbunden. Elektronen, die auf der Seite des n-Typs erzeugt oder auf der Seite des p-Typs erzeugt, durch die Verbindung „gesammelt“ und auf die Seite des n-Typs geschwenkt werden, können durch den Draht wandern, die Last mit Energie versorgen und durch den Draht fortfahren bis sie den p-Typ-Halbleiter-Metall-Kontakt erreichen. Hier rekombinieren sie mit einem Loch, das entweder als ein Elektron-Loch-Paar auf der p-Typ-Seite der Solarzelle erzeugt wurde, oder ein Loch, das von der n-Typ-Seite über die Verbindung gefegt wurde, nachdem es dort erzeugt wurde.

Die gemessene Spannung ist gleich der Differenz der Quasi-Fermi-Niveaus der Majoritätsträger (Elektronen in dem n-Typ-Teil und Löcher in dem p-Typ-Teil) an den zwei Anschlüssen.

Äquivalente Schaltung einer Solarzelle
Um das elektronische Verhalten einer Solarzelle zu verstehen, ist es nützlich, ein Modell zu erstellen, das elektrisch äquivalent ist und auf diskreten idealen elektrischen Komponenten basiert, deren Verhalten gut definiert ist. Eine ideale Solarzelle kann durch eine Stromquelle parallel zu einer Diode modelliert werden; In der Praxis ist keine Solarzelle ideal, daher werden dem Modell ein Shunt-Widerstand und eine Serienwiderstandskomponente hinzugefügt. Das resultierende Ersatzschaltbild einer Solarzelle ist links abgebildet. Rechts dargestellt ist auch die schematische Darstellung einer Solarzelle zur Verwendung in Schaltplänen.

Charakteristische Gleichung
Aus der Ersatzschaltung ist ersichtlich, dass der von der Solarzelle erzeugte Strom gleich dem Strom ist, der von der Stromquelle erzeugt wird, minus dem Strom, der durch die Diode fließt, minus dem Strom, der durch den Shunt-Widerstand fließt:

woher
I = Ausgangsstrom (Ampere)
I _L = photogenerierter Strom (Ampere)
I _D = Diodenstrom (Ampere)
I _SH = Nebenschlussstrom (Ampere).

Der Strom durch diese Elemente wird durch die Spannung über sie bestimmt:

woher
V _j = Spannung über Diode und Widerstand RSH (Volt)
V = Spannung an den Ausgangsklemmen (Volt)
I = Ausgangsstrom (Ampere)
R _S = Serienwiderstand (Ω).

Nach der Shockley-Diodengleichung ist der durch die Diode abgeleitete Strom:

woher
I ₀ = umgekehrter Sättigungsstrom (Ampere)
n = Diodenidealitätsfaktor (1 für eine ideale Diode)
q = Elementarladung
k = Boltzmanns Konstante
T = absolute Temperatur

 die thermische Spannung. Bei 25 ° C  Volt.
Nach dem Ohmschen Gesetz ist der durch den Shunt-Widerstand abgeleitete Strom:

woher
R _SH = Shuntwiderstand (Ω).

Durch Einsetzen in die erste Gleichung wird die charakteristische Gleichung einer Solarzelle erzeugt, die die Solarzellenparameter mit dem Ausgangsstrom und der Ausgangsspannung in Beziehung setzt:

Eine alternative Herleitung erzeugt eine ähnliche Gleichung, aber mit V auf der linken Seite. Die zwei Alternativen sind Identitäten; Das heißt, sie liefern genau die gleichen Ergebnisse.

Da die Parameter I ₀ , n, R _S und R _SH nicht direkt gemessen werden können, ist die häufigste Anwendung der charakteristischen Gleichung die nichtlineare Regression, um die Werte dieser Parameter auf der Grundlage ihrer kombinierten Wirkung auf das Solarzellenverhalten zu extrahieren.

Wenn RS nicht Null ist, ergibt die obige Gleichung nicht direkt den Strom I, aber sie kann dann mit der Lambert-W-Funktion gelöst werden:

Wenn eine externe Last mit der Zelle verwendet wird, kann ihr Widerstand einfach zu RS addiert und V auf Null gesetzt werden, um den Strom zu finden.

Wenn R _SH unendlich ist, gibt es eine Lösung für V für alle  weniger als  :

Ansonsten kann man mit der Lambert-W-Funktion nach V auflösen:

Wenn R _SH jedoch groß ist, ist es besser, die ursprüngliche Gleichung numerisch zu lösen.
Die allgemeine Form der Lösung ist eine Kurve, wobei I abnimmt, wenn V ansteigt. Die Steigung bei kleinem oder negativem V (wo die W- Funktion nahe Null ist) nähert sich , während sich die Steigung bei hohem V nähert  .

Leerlaufspannung und Kurzschlussstrom
Wenn die Zelle in einem offenen Stromkreis betrieben wird, ist I = 0 und die Spannung an den Ausgangsanschlüssen ist als die Leerlaufspannung definiert . Unter der Annahme, dass der Shunt-Widerstand hoch genug ist, um den letzten Term der charakteristischen Gleichung zu vernachlässigen, ist die Leerlaufspannung V _OC :

In ähnlicher Weise wird, wenn die Zelle bei einem Kurzschluss betrieben wird, V = 0 und der Strom I durch die Anschlüsse als der Kurzschlussstrom definiert. Es kann gezeigt werden, dass für eine hochqualitative Solarzelle (niedriger R _S und I ₀ und hoher R _SH ) der Kurzschlussstrom I _SC ist:

Es ist nicht möglich, dem Gerät Strom zu entnehmen, wenn es unter Leerlauf- oder Kurzschlussbedingungen arbeitet.

Wirkung der physikalischen Größe
Die Werte von IL, I0, RS und RSH hängen von der physikalischen Größe der Solarzelle ab. Beim Vergleich von ansonsten identischen Zellen wird eine Zelle mit der doppelten Übergangsfläche eines anderen im Prinzip das Doppelte von IL und I0 haben, weil sie die doppelte Fläche aufweist, in der der Photostrom erzeugt wird und über die Diodenstrom fließen kann. Mit dem gleichen Argument wird es auch die Hälfte der RS ​​des Serienwiderstandes in Bezug auf den vertikalen Stromfluss haben; Bei großflächigen Siliziumsolarzellen ist die Skalierung des Serienwiderstandes durch den lateralen Stromfluss jedoch nicht leicht vorhersagbar, da dies entscheidend vom Gitterdesign abhängt (es ist nicht klar, was „ansonsten identisch“ in dieser Hinsicht bedeutet). Abhängig vom Shunt-Typ kann die größere Zelle auch die Hälfte des RSH haben, da sie die doppelte Fläche hat, in der Shunts auftreten können; Auf der anderen Seite, wenn Shunts hauptsächlich am Umfang auftreten, wird RSH entsprechend der Änderung des Umfangs, nicht des Bereichs abnehmen.

Da die Änderungen der Ströme dominierend sind und sich gegenseitig ausgleichen, ist die Leerlaufspannung praktisch gleich; VOC hängt nur dann von der Zellengröße ab, wenn RSH zu niedrig wird. Um die Dominanz der Ströme zu berücksichtigen, wird die charakteristische Gleichung häufig in Bezug auf die Stromdichte oder den Strom geschrieben, der pro Einheitszellenfläche erzeugt wird:

woher
J = Stromdichte (Ampere / cm ² )
J _L = photoerzeugte Stromdichte (Ampere / cm ² )
J ₀ = umgekehrte Sättigungsstromdichte (Ampere / cm ² )
r _S = spezifischer Serienwiderstand (Ω-cm ² )
r _SH = spezifischer Shuntwiderstand (Ω-cm ² ).

Diese Formulierung hat mehrere Vorteile. Da Zelleneigenschaften auf eine gemeinsame Querschnittsfläche bezogen sind, können sie für Zellen unterschiedlicher physikalischer Abmessungen verglichen werden. Während dies in einem Herstellungsumfeld, in dem alle Zellen dazu neigen, die gleiche Größe zu haben, von begrenztem Nutzen ist, ist es nützlich in der Forschung und beim Vergleichen von Zellen zwischen Herstellern. Ein weiterer Vorteil besteht darin, dass die Dichtegleichung die Parameterwerte natürlich auf ähnliche Größenordnungen skaliert, was die numerische Extraktion derselben sogar mit naiven Lösungsmethoden einfacher und genauer machen kann.

Es gibt praktische Einschränkungen dieser Formulierung. Zum Beispiel gewinnen bestimmte parasitäre Effekte an Bedeutung, wenn die Zellgrößen schrumpfen und die extrahierten Parameterwerte beeinflussen können. Die Rekombination und die Kontamination der Verbindung sind tendenziell am größten am Umfang der Zelle, so dass sehr kleine Zellen höhere Werte von J0 oder niedrigere Werte von RSH aufweisen können als größere Zellen, die ansonsten identisch sind.In solchen Fällen müssen Vergleiche zwischen Zellen vorsichtig und mit diesen Auswirkungen gemacht werden.
Dieser Ansatz sollte nur zum Vergleich von Solarzellen mit vergleichbarem Layout verwendet werden. Zum Beispiel kann ein Vergleich zwischen primär quadratischen Solarzellen wie typischen kristallinen Siliziumsolarzellen und schmalen, aber langen Solarzellen wie typischen Dünnschichtsolarzellen zu falschen Annahmen führen, die durch die unterschiedlichen Arten von Strompfaden verursacht werden, und somit zum Beispiel den Einfluss von ein verteilter Serienwiderstandsbeitrag zu rS. Die Makroarchitektur der Solarzellen könnte dazu führen, dass unterschiedliche Oberflächen in jedem festen Volumen angeordnet werden – insbesondere für Dünnschichtsolarzellen und flexible Solarzellen, die hochkonvolut gefaltete Strukturen ermöglichen können. Wenn Volumen die Bindungsbeschränkung ist, dann kann die auf der Oberfläche basierende Effizienzdichte von geringerer Relevanz sein.

Transparente leitende Elektroden
Transparente Leitelektroden sind essentielle Bestandteile von Solarzellen. Es ist entweder ein kontinuierlicher Film aus Indiumzinnoxid oder ein leitendes Drahtnetzwerk, in dem Drähte Ladungskollektoren sind, während Hohlräume zwischen Drähten für Licht transparent sind. Eine optimale Dichte des Drahtnetzwerkes ist wesentlich für die maximale Solarzellenleistung, da eine höhere Drahtdichte die Lichtdurchlässigkeit blockiert, während eine geringere Drahtdichte aufgrund der größeren Entfernung durch die Ladungsträger zu hohen Rekombinationsverlusten führt.

Zelltemperatur
Die Temperatur beeinflusst die charakteristische Gleichung auf zwei Arten: direkt, über T im exponentiellen Term und indirekt über ihre Wirkung auf I0 (streng genommen wirkt sich die Temperatur auf alle Terme aus, aber diese beiden sind weitaus signifikanter als die anderen).Während das Erhöhen von T die Größe des Exponenten in der charakteristischen Gleichung verringert, steigt der Wert von I0 exponentiell mit T. Der Nettoeffekt ist, die VOC (die Leerlaufspannung) linear mit steigender Temperatur zu reduzieren. Die Größenordnung dieser Verringerung ist umgekehrt proportional zu VOC; das heißt, Zellen mit höheren VOC-Werten erleiden kleinere Spannungsabfälle mit steigender Temperatur. Für die meisten kristallinen Siliziumsolarzellen beträgt die Änderung der VOC mit der Temperatur etwa -0,50% / ° C, obwohl die Rate für die kristallinen Siliziumzellen mit der höchsten Effizienz etwa -0,35% / ° C beträgt. Zum Vergleich beträgt die Rate für Solarzellen aus amorphem Silizium -0,20% / ° C bis -0,30% / ° C, abhängig davon, wie die Zelle hergestellt ist.

Die Menge an mit Licht erzeugtem Strom IL nimmt mit zunehmender Temperatur aufgrund einer Zunahme der Anzahl thermisch erzeugter Träger in der Zelle leicht zu. Dieser Effekt ist jedoch gering: etwa 0,065% / ºC für kristalline Siliziumzellen und 0,09% für amorphe Siliziumzellen.

Der Gesamteffekt der Temperatur auf die Zelleffizienz kann unter Verwendung dieser Faktoren in Kombination mit der charakteristischen Gleichung berechnet werden. Da jedoch die Änderung der Spannung viel stärker ist als die Änderung des Stroms, neigt die Gesamtwirkung auf den Wirkungsgrad dazu, ähnlich der Spannung zu sein. Die meisten kristallinen Silizium-Solarzellen nehmen um 0,50% / ° C ab und die meisten amorphen Zellen fallen um 0,15-0,25% / ° C ab. Die obige Abbildung zeigt IV-Kurven, die typischerweise für eine kristalline Silizium-Solarzelle bei verschiedenen Temperaturen zu sehen sind.

Serienwiderstand
Wenn der Reihenwiderstand ansteigt, wird der Spannungsabfall zwischen der Übergangsspannung und der Klemmenspannung für den gleichen Strom größer. Das Ergebnis ist, dass der stromgesteuerte Teil der IV-Kurve beginnt, sich zum Ursprung hin abzusenken, was zu einer signifikanten Abnahme der Klemmenspannung führt  und eine leichte Verringerung der ISC, der Kurzschlussstrom. Sehr hohe RS-Werte führen auch zu einer signifikanten Verringerung der ISC; In diesen Regimen dominiert der Serienwiderstand und das Verhalten der Solarzelle ähnelt dem eines Widerstands. Diese Effekte werden für kristalline Siliziumsolarzellen in den IV-Kurven gezeigt, die in der Abbildung rechts dargestellt sind.

Durch den Serienwiderstand verursachte Verluste werden in erster Näherung durch P _loss = V _Rs I = I² R _{S gegeben} und steigen quadratisch mit (Foto-) Strom an. Serienwiderstandsverluste sind daher bei hohen Beleuchtungsintensitäten am wichtigsten.

Shunt-Widerstand
Wenn der Shunt-Widerstand abnimmt, steigt der Strom, der durch den Shunt-Widerstand abgeleitet wird, für einen gegebenen Pegel der Übergangsspannung an. Das Ergebnis ist, dass der spannungsgesteuerte Teil der IV-Kurve beginnt, weit vom Ursprung abzusinken, was zu einer signifikanten Abnahme des Anschlussstroms I und einer leichten Verringerung der VOC führt. Sehr niedrige RSH-Werte führen zu einer signifikanten Verringerung der VOC. Ähnlich wie bei einem hohen Serienwiderstand nimmt eine schlecht parallel geschaltete Solarzelle ähnliche Betriebseigenschaften an wie ein Widerstand. Diese Effekte werden für kristalline Siliziumsolarzellen in den IV-Kurven gezeigt, die in der Abbildung rechts dargestellt sind.

Sättigungsstrom umkehren
Wenn man von einem unendlichen Shunt-Widerstand ausgeht, kann die charakteristische Gleichung für V _OC gelöst werden:

Somit führt eine Zunahme von I0 zu einer Verringerung der VOC proportional zur Umkehrung des Logarithmus der Zunahme. Dies erklärt mathematisch den Grund für die Verringerung der VOC, die mit den oben beschriebenen Temperaturerhöhungen einhergeht. Der Effekt des umgekehrten Sättigungsstroms auf die IV-Kurve einer kristallinen Silizium-Solarzelle ist in der Abbildung rechts dargestellt. Physikalisch ist der umgekehrte Sättigungsstrom ein Maß für das „Lecken“ von Ladungsträgern über den pn-Übergang in Sperrspannung. Diese Leckage ist ein Ergebnis der Ladungsträgerrekombination in den neutralen Regionen auf jeder Seite der Verbindung.

Idealitätsfaktor
Der Idealitätsfaktor (auch Emissivitätsfaktor genannt) ist ein passender Parameter, der beschreibt, wie genau das Verhalten der Diode dem von der Theorie vorhergesagten entspricht, wobei angenommen wird, dass der pn-Übergang der Diode eine unendliche Ebene ist und keine Rekombination innerhalb der Raumladungszone stattfindet. Eine perfekte Übereinstimmung mit der Theorie ist gegeben, wenn n = 1 ist. Wenn die Rekombination in der Raumladungszone eine andere Rekombination dominiert, ist jedoch n = 2. Der Effekt der Änderung des idealen Faktors unabhängig von allen anderen Parametern ist für eine kristalline Siliziumsolarzelle gezeigt Die IV-Kurven werden in der Abbildung rechts angezeigt.

Die meisten Solarzellen, die im Vergleich zu herkömmlichen Dioden ziemlich groß sind, nähern sich einer unendlichen Ebene gut an und zeigen normalerweise ein nahezu ideales Verhalten unter Standardtestbedingungen (n ≥ 1). Unter bestimmten Betriebsbedingungen kann jedoch der Betrieb der Vorrichtung durch Rekombination in der Raumladungszone dominiert werden. Dies ist durch einen signifikanten Anstieg von I0 sowie eine Erhöhung des Idealitätsfaktors auf n ≥ 2 gekennzeichnet. Letzterer tendiert dazu, die Solarzellen-Ausgangsspannung zu erhöhen, während die erstere dazu dient, sie zu erodieren. Der Nettoeffekt ist daher eine Kombination aus der Zunahme der Spannung, die für das Erhöhen von n in der Figur nach rechts gezeigt ist, und der Abnahme der Spannung, die für das Erhöhen von I0 in der obigen Figur gezeigt ist. Typischerweise ist I0 der signifikantere Faktor und das Ergebnis ist eine Verringerung der Spannung.

Manchmal wird beobachtet, dass der Idealitätsfaktor größer als 2 ist, was im Allgemeinen der Anwesenheit von Schottky-Diode oder Heteroübergang in der Solarzelle zugeschrieben wird. Das Vorhandensein eines Heterojunction-Offsets verringert die Sammeleffizienz der Solarzelle und kann zu einem geringen Füllfaktor beitragen.