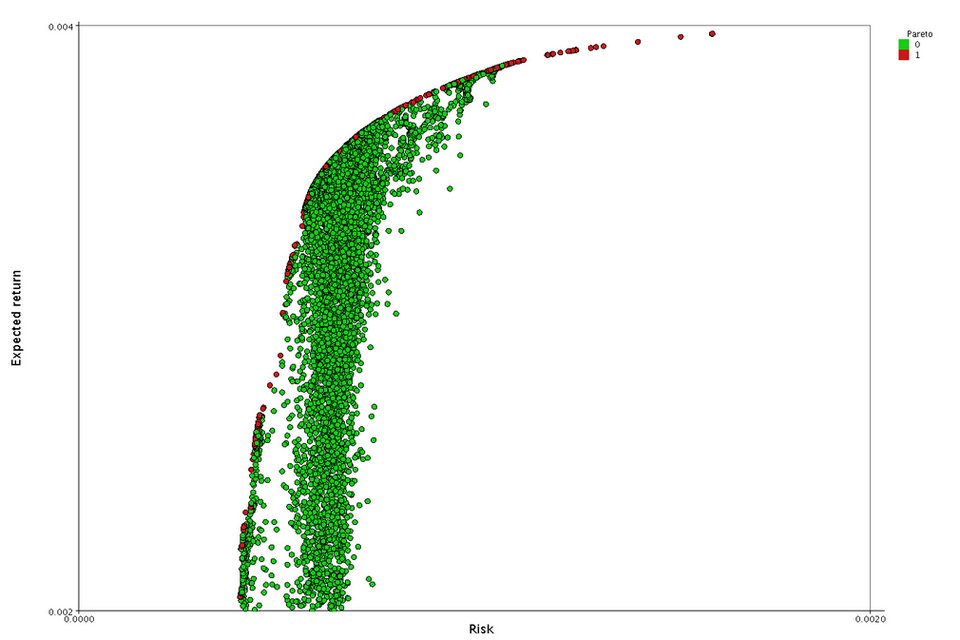
Multiple-Kriterien-Entscheidungsfindung (MCDM) oder Multi-Kriterien-Entscheidung Analyse (MCDA) ist eine Teildisziplin der Operations Research, die explizit mehrere widersprüchliche Kriterien bei der Entscheidungsfindung (sowohl im täglichen Leben und in Einstellungen wie Unternehmen, Regierung und Medizin ). Widersprüchliche Kriterien sind typisch für die Bewertung von Optionen: Kosten oder Preise sind normalerweise eines der Hauptkriterien, und ein gewisses Maß an Qualität ist typischerweise ein anderes Kriterium, das leicht in Konflikt mit den Kosten steht. Beim Kauf eines Autos können Kosten, Komfort, Sicherheit und Kraftstoffverbrauch einige der Hauptkriterien sein, die wir in Betracht ziehen – es ist ungewöhnlich, dass das billigste Auto das bequemste und das sicherste ist. Im Portfoliomanagement sind wir daran interessiert, hohe Renditen zu erzielen, gleichzeitig aber auch unsere Risiken zu reduzieren, aber die Aktien, die das Potenzial haben, hohe Renditen zu erzielen, sind in der Regel auch mit hohen Verlusten verbunden. In einer Dienstleistungsbranche sind die Kundenzufriedenheit und die Kosten für die Erbringung von Dienstleistungen grundlegende widersprüchliche Kriterien.

In unserem täglichen Leben gewichten wir normalerweise mehrere Kriterien implizit und wir können mit den Folgen solcher Entscheidungen vertraut sein, die nur auf Intuition beruhen. Auf der anderen Seite ist es wichtig, wenn das Problem hoch ist, das Problem richtig zu strukturieren und mehrere Kriterien explizit zu bewerten. Bei der Entscheidung, ob ein Atomkraftwerk gebaut werden soll oder nicht, gibt es nicht nur sehr komplexe Fragen, die mehrere Kriterien beinhalten, sondern es gibt auch mehrere Parteien, die von den Konsequenzen stark betroffen sind.

Komplexe Probleme gut zu strukturieren und multiple Kriterien zu berücksichtigen, führt explizit zu fundierteren und besseren Entscheidungen. Seit Beginn der modernen Entscheidungsfindung mit mehreren Kriterien in den frühen 1960er Jahren sind auf diesem Gebiet wichtige Fortschritte erzielt worden. Eine Vielzahl von Ansätzen und Methoden, von denen viele durch spezialisierte Entscheidungssoftware implementiert wurden, wurde für ihre Anwendung in einer Reihe von Disziplinen entwickelt, die von Politik und Wirtschaft bis zu Umwelt und Energie reichen.

Grundlagen, Konzepte, Definitionen
MCDM oder MCDA sind wohlbekannte Akronyme für die Entscheidungsfindung mit mehreren Kriterien und die Entscheidungsanalyse mit mehreren Kriterien; Stanley Zionts half, das Akronym mit seinem 1979 erschienenen Artikel „MCDM – Wenn nicht eine römische Zahl, dann was?“ Populär zu machen, der für ein unternehmerisches Publikum bestimmt ist.

MCDM befasst sich mit der Strukturierung und Lösung von Entscheidungs- und Planungsproblemen mit mehreren Kriterien. Ziel ist es, Entscheidungsträger bei solchen Problemen zu unterstützen. Typischerweise gibt es keine einzigartige optimale Lösung für solche Probleme und es ist notwendig, die Präferenzen des Entscheidungsträgers zu verwenden, um zwischen Lösungen zu unterscheiden.

„Lösen“ kann auf verschiedene Arten interpretiert werden. Es könnte der Auswahl der „besten“ Alternative aus einer Reihe verfügbarer Alternativen entsprechen (wobei „beste“ als „die am meisten bevorzugte Alternative“ eines Entscheidungsträgers interpretiert werden kann). Eine andere Interpretation von „lösen“ könnte die Auswahl einer kleinen Menge guter Alternativen oder das Gruppieren von Alternativen in verschiedene Präferenzsätze sein. Eine extreme Interpretation könnte darin bestehen, alle „effizienten“ oder „nicht-dominierten“ Alternativen zu finden (die wir in Kürze definieren werden).

Die Schwierigkeit des Problems beruht auf dem Vorhandensein von mehr als einem Kriterium. Es gibt nicht länger eine einzigartige optimale Lösung für ein MCDM-Problem, die ohne Einbeziehung von Präferenzinformationen erhalten werden kann. Das Konzept einer optimalen Lösung wird oft durch den Satz nicht kombinierter Lösungen ersetzt. Eine nicht-dominierte Lösung hat die Eigenschaft, dass sie sich nicht von einer anderen Lösung wegbewegen kann, ohne mindestens ein Kriterium zu verlieren. Daher ist es für den Entscheider sinnvoll, eine Lösung aus dem nicht-dominierten Set zu wählen. Ansonsten könnte er / sie in Bezug auf einige oder alle der Kriterien besser sein und sich in keinem von ihnen schlechter schlagen. Im Allgemeinen ist jedoch der Satz nicht kombinierter Lösungen zu groß, um dem Entscheidungsträger für die endgültige Auswahl präsentiert zu werden. Daher brauchen wir Werkzeuge, die dem Entscheidungsträger helfen, sich auf die bevorzugten Lösungen (oder Alternativen) zu konzentrieren. Normalerweise muss man bestimmte Kriterien für andere „abwägen“.

MCDM ist seit den 1970er Jahren ein aktives Forschungsgebiet. Es gibt mehrere MCDM-bezogene Organisationen, darunter die Internationale Gesellschaft für Multi-Kriterien-Entscheidungsfindung, die Euro-Arbeitsgruppe für MCDA und die INFORMS-Sektion für MCDM. Für eine Geschichte siehe: Köksalan, Wallenius und Zionts (2011). MCDM stützt sich auf Wissen in vielen Bereichen, einschließlich:

Mathematik
Entscheidungsanalyse
Wirtschaft
Computertechnologie
Softwareentwicklung
Informationssysteme

Eine Typologie
Es gibt verschiedene Klassifikationen von MCDM-Problemen und -Methoden. Ein Hauptunterschied zwischen MCDM-Problemen basiert darauf, ob die Lösungen explizit oder implizit definiert sind.

Bewertungsprobleme mit mehreren Kriterien: Diese Probleme bestehen aus einer endlichen Anzahl von Alternativen, die zu Beginn des Lösungsprozesses explizit bekannt sind. Jede Alternative wird durch ihre Leistung in mehreren Kriterien dargestellt. Das Problem kann definiert werden als das Finden der besten Alternative für einen Entscheidungsträger (DM) oder das Finden einer Reihe von guten Alternativen. Man könnte auch daran interessiert sein, Alternativen zu „sortieren“ oder zu „klassifizieren“. Das Sortieren bezieht sich auf das Platzieren von Alternativen in einer Reihe von nach Präferenz geordneten Klassen (z. B. Zuweisen von Kreditbewertungen zu Ländern), und das Klassifizieren bezieht sich auf das Zuweisen von Alternativen zu nicht geordneten Mengen (z. B. Diagnostizieren von Patienten anhand ihrer Symptome). Einige der MCDM-Methoden in dieser Kategorie wurden in dem Buch von Triantaphyllou 2000 zu diesem Thema vergleichend untersucht.
Designprobleme mit mehreren Kriterien (mehrere objektive mathematische Programmierprobleme): Bei diesen Problemen sind die Alternativen nicht explizit bekannt. Eine Alternative (Lösung) kann durch Lösen eines mathematischen Modells gefunden werden. Die Anzahl der Alternativen ist entweder unendlich und nicht zählbar (wenn einige Variablen kontinuierlich sind) oder typischerweise sehr groß, wenn zählbar (wenn alle Variablen diskret sind).
Ob es sich um ein Bewertungsproblem oder ein Entwurfsproblem handelt, die Präferenzinformation von DMs ist erforderlich, um zwischen Lösungen zu unterscheiden. Die Lösungsverfahren für MCDM-Probleme werden üblicherweise basierend auf dem Timing von Präferenzinformationen klassifiziert, die von dem DM erhalten werden.

Es gibt Methoden, die zu Beginn des Prozesses die Präferenzinformationen des DM benötigen und das Problem in ein einziges Kriteriumsproblem verwandeln. Man sagt, dass diese Methoden durch „vorherige Artikulation von Präferenzen“ funktionieren. Verfahren, die auf der Schätzung einer Wertfunktion oder der Verwendung des Konzepts der „Out-Ranking-Relationen“, des analytischen Hierarchieprozesses und einiger entscheidungsregelbasierter Verfahren basieren, versuchen, mehrere Kriterienbewertungsprobleme unter Verwendung vorheriger Artikulation von Präferenzen zu lösen. In ähnlicher Weise gibt es Verfahren, die entwickelt werden, um Designprobleme mehrerer Kriterien zu lösen, indem die Präferenzen vorher gelenkt werden, indem eine Wertfunktion konstruiert wird. Die wohl bekannteste dieser Methoden ist die Zielprogrammierung. Sobald die Wertfunktion konstruiert ist, wird das resultierende mathematische Einzelzielprogramm gelöst, um eine bevorzugte Lösung zu erhalten.

Einige Methoden erfordern Präferenzinformationen vom DM während des gesamten Lösungsprozesses. Diese werden als interaktive Methoden oder Methoden bezeichnet, die eine „progressive Artikulation von Präferenzen“ erfordern. Diese Verfahren sind sowohl für die Bewertung mehrerer Kriterien (siehe beispielsweise Geoffrion, Dyer und Feinberg, 1972, und Köksalan und Sagala, 1995) als auch für Designprobleme (siehe Steuer, 1986) gut entwickelt worden.

Designprobleme mit mehreren Kriterien erfordern typischerweise die Lösung einer Reihe mathematischer Programmiermodelle, um implizit definierte Lösungen aufzudecken. Für diese Probleme könnte auch eine Darstellung oder Annäherung von „effizienten Lösungen“ von Interesse sein. Diese Kategorie wird als „posterior articulation of preferences“ bezeichnet, was impliziert, dass die Beteiligung der DM hinter der expliziten Offenbarung „interessanter“ Lösungen beginnt (siehe zum Beispiel Karasakal und Köksalan, 2009).

Wenn die mathematischen Programmiermodelle Integer-Variablen enthalten, werden die Entwurfsprobleme schwieriger zu lösen. Die multi-objektive kombinatorische Optimierung (MOCO) stellt eine spezielle Kategorie solcher Probleme dar, die erhebliche Rechenschwierigkeiten aufweisen (siehe Ehrgott und Gandibleux, 2002, für eine Übersicht).

Darstellungen und Definitionen
Das MCDM-Problem kann im Kriterienraum oder im Entscheidungsraum dargestellt werden. Wenn alternativ verschiedene Kriterien durch eine gewichtete lineare Funktion kombiniert werden, ist es auch möglich, das Problem im Gewichtungsraum darzustellen. Im Folgenden finden Sie die Demonstrationen der Kriterien und Gewichtsräume sowie einige formale Definitionen.

Kriterium Raumdarstellung

Nehmen wir an, wir evaluieren Lösungen in einer spezifischen Problemsituation anhand mehrerer Kriterien. Nehmen wir weiterhin an, dass mehr in jedem Kriterium besser ist. Dann sind wir unter allen möglichen Lösungen ideal an Lösungen interessiert, die in allen berücksichtigten Kriterien gut funktionieren. Es ist jedoch unwahrscheinlich, dass es eine einzige Lösung gibt, die in allen berücksichtigten Kriterien gut abschneidet. In der Regel weisen einige Lösungen bei einigen Kriterien eine gute Leistung auf, während andere bei anderen gute Ergebnisse erzielen. Einen Weg zwischen den Kriterien zu finden, ist eines der Hauptanliegen der MCDM-Literatur.

Mathematisch kann das MCDM-Problem, das den obigen Argumenten entspricht, als dargestellt werden

„max“ q
unterliegt
q ∈ Q
wo q ist der Vektor von k-Kriterium Funktionen (Zielfunktionen) und Q ist die machbare Menge, Q ⊆ Rk.

Wenn Q explizit (durch eine Reihe von Alternativen) definiert ist, wird das resultierende Problem als Multiple Criteria Evaluation-Problem bezeichnet.

Wenn Q implizit definiert ist (durch eine Reihe von Einschränkungen), wird das resultierende Problem als Multiple Criteria Design-Problem bezeichnet.

Die Anführungszeichen werden verwendet, um anzuzeigen, dass die Maximierung eines Vektors keine wohldefinierte mathematische Operation ist. Dies entspricht dem Argument, dass wir einen Weg finden müssen, den Kompromiss zwischen den Kriterien zu lösen (typischerweise basierend auf den Präferenzen eines Entscheidungsträgers), wenn eine Lösung, die in allen Kriterien gut funktioniert, nicht existiert.

Repräsentationsraumdarstellung

Der Entscheidungsraum entspricht der Menge möglicher Entscheidungen, die uns zur Verfügung stehen. Die Kriterienwerte werden Konsequenzen unserer Entscheidungen sein. Daher können wir ein entsprechendes Problem im Entscheidungsraum definieren. Bei der Gestaltung eines Produkts entscheiden wir beispielsweise über die Designparameter (Entscheidungsvariablen), von denen jede die Leistungskriterien (Kriterien) beeinflusst, mit denen wir unser Produkt bewerten.

Mathematisch kann ein Designproblem mit mehreren Kriterien wie folgt im Entscheidungsraum dargestellt werden:

„max“ q = f (x) = (f1 (x), …, fk (x))
unterliegt
q ∈ Q = {f (x): x ∈ X, X ∈ Rn},
wobei X die zulässige Menge und x der Vektor der Entscheidungsvariablen der Größe n ist.

Ein gut entwickelter Spezialfall wird erhalten, wenn X ein Polyeder ist, das durch lineare Ungleichungen und Gleichheiten definiert ist. Wenn alle Zielfunktionen bezüglich der Entscheidungsvariablen linear sind, führt diese Variation zu einer mehrfachen objektiven linearen Programmierung (MOLP), einer wichtigen Unterklasse von MCDM-Problemen.

Es gibt mehrere Definitionen, die in MCDM von zentraler Bedeutung sind. Zwei eng verwandte Definitionen sind die der Nicht-Dominanz (definiert auf der Grundlage der Raum-Repräsentation des Kriteriums) und der Effizienz (basierend auf der Repräsentation der Entscheidungsvariablen).

Definition 1. q * ∈ Q ist nicht dominierend, wenn es kein anderes q ∈ Q gibt, so dass q ≥ q * und q ∈ q *.

Grob gesagt, ist eine Lösung nicht geduldet, solange sie keiner anderen verfügbaren Lösung in allen berücksichtigten Kriterien nachsteht.

Definition 2. x * ∈ X ist effizient, wenn kein anderes x ∈ X existiert, so dass f (x) ≥ f (x *) und f (x) ≠ f (x *).

Wenn ein MCDM-Problem eine Entscheidungssituation gut darstellt, dann muss die am meisten bevorzugte Lösung einer DM eine effiziente Lösung im Entscheidungsraum sein, und ihr Bild ist ein nicht-kombinierter Punkt im Kriterienraum. Die folgenden Definitionen sind ebenfalls wichtig.

Definition 3. q * ∈ Q ist schwach nichtdominiert, wenn es kein anderes q ∈ Q gibt, so dass q> q *.

Definition 4. x * ∞ X ist schwach effizient, wenn kein anderes x ∈ X existiert, so dass f (x)> f (x *).

Schwach nicht verbundene Punkte umfassen alle nicht-dominierten Punkte und einige spezielle dominierte Punkte. Die Bedeutung dieser speziellen dominierten Punkte ergibt sich aus der Tatsache, dass sie in der Praxis häufig auftreten und besondere Sorgfalt erforderlich ist, um sie von nicht-dominierten Punkten zu unterscheiden. Wenn wir zum Beispiel ein einzelnes Ziel maximieren, erhalten wir möglicherweise einen schwach dominierten Punkt, der dominiert wird. Die dominierten Punkte der schwach nicht dominierten Menge befinden sich entweder auf vertikalen oder horizontalen Ebenen (Hyperebenen) im Kriteriumsraum.

Idealer Punkt: (im Kriteriumsraum) repräsentiert das Beste (das Maximum für Maximierungsprobleme und das Minimum für Minimierungsprobleme) jeder Zielfunktion und entspricht typischerweise einer nicht realisierbaren Lösung.

Nadir-Punkt: (im Kriteriumsraum) repräsentiert das schlechteste (das Minimum für Maximierungsprobleme und das Maximum für Minimierungsprobleme) jeder Zielfunktion unter den Punkten in der nicht-dominierten Menge und ist typischerweise ein dominierter Punkt.

Der ideale Punkt und der Nadirpunkt sind für den DM nützlich, um das „Gefühl“ des Lösungsbereichs zu erhalten (obwohl es nicht einfach ist, den Nadirpunkt für Konstruktionsprobleme mit mehr als zwei Kriterien zu finden).

Abbildungen der Entscheidungs- und Kriteriumsräume

Das folgende MOLP-Problem mit zwei Variablen im Entscheidungsvariablenraum hilft, einige der Schlüsselkonzepte grafisch darzustellen.

Max f1 (x) = -x1 + 2×2
Max f2 (x) = 2×1 – x2
unterliegt
x1 ≤ 4
x2 ≤ 4
x1 + x2 ≤ 7
-x1 + x2 ≤ 3
x1 – x2 ≤ 3
x1, x2 ≥ 0

In Fig. 1 maximieren die Extrempunkte „e“ und „b“ die ersten bzw. zweiten Ziele. Die rote Grenze zwischen diesen beiden Extrempunkten repräsentiert die effiziente Menge. Aus der Abbildung ist ersichtlich, dass es für jede mögliche Lösung außerhalb der effizienten Menge möglich ist, beide Ziele um einige Punkte in der effizienten Menge zu verbessern. Umgekehrt ist es für keinen Punkt auf dem effizienten Set möglich, beide Ziele zu verbessern, indem auf irgendeine andere mögliche Lösung übergegangen wird. Bei diesen Lösungen muss man von einem der Ziele opfern, um das andere Ziel zu verbessern.

Aufgrund seiner Einfachheit kann das obige Problem im Kriteriumsraum dargestellt werden, indem die x mit den f wie folgt ersetzt werden:

Max f1
Max. F2
unterliegt
f1 + 2f2 ≤ 12
2f1 + f2 ≤ 12
f1 + f2 ≤ 7
f1 – f2 ≤ 9
-f1 + f2 ≤ 9
f1 + 2f2 ≥ 0
2f1 + f2 ≥ 0
Wir präsentieren den Kriteriumsraum in Abbildung 2 graphisch. Es ist einfacher, die nicht verknüpften Punkte (entsprechend effizienten Lösungen im Entscheidungsraum) im Kriteriumsraum zu erkennen. Die Region im Nordosten des durchführbaren Raums bildet die Menge nicht kombinierter Punkte (für Maximierungsprobleme).

Generieren nicht-kombinierter Lösungen
Es gibt mehrere Möglichkeiten, nicht-dominierte Lösungen zu generieren. Wir werden zwei davon besprechen. Der erste Ansatz kann eine spezielle Klasse nicht kombinierter Lösungen erzeugen, während der zweite Ansatz jede nicht-dominierte Lösung erzeugen kann.

Gewichtete Beträge (Gass & Saaty, 1955)
Kombinieren wir die Mehrfachkriterien zu einem einzigen Kriterium, indem wir jedes Kriterium mit einem positiven Gewicht multiplizieren und die gewichteten Kriterien aufaddieren, dann ist die Lösung des resultierenden Einzelkriteriums eine besonders effiziente Lösung. Diese speziellen effizienten Lösungen erscheinen an den Eckpunkten der verfügbaren Lösungen. Effiziente Lösungen, die nicht an Eckpunkten liegen, haben besondere Eigenschaften und diese Methode ist nicht in der Lage, solche Punkte zu finden. Mathematisch können wir diese Situation als darstellen

max wT.q = wT.f (x), w> 0
unterliegt
x ∈ X
Durch Variieren der Gewichtungen können gewichtete Summen zum Erzeugen von effizienten Extrempunktlösungen für Entwurfsprobleme und unterstützte (konvex nicht verbundene) Punkte für Bewertungsprobleme verwendet werden.

Leistungsskalierungsfunktion (Wierzbicki, 1980)

Leistungsskalarisierende Funktionen kombinieren auch mehrere Kriterien zu einem einzigen Kriterium, indem sie diese auf eine ganz spezielle Weise gewichten. Sie erzeugen rechteckige Konturen, die von einem Bezugspunkt zu den verfügbaren effizienten Lösungen gehen. Diese spezielle Struktur ermöglicht Leistungsskalierungsfunktionen, um jede effiziente Lösung zu erreichen. Dies ist eine mächtige Eigenschaft, die diese Funktionen für MCDM-Probleme sehr nützlich macht.

Mathematisch können wir das entsprechende Problem als darstellen

Min s (g, q, w, ρ) = Min {maxi [(gi – qi) / wi] + ρi (gi-qi)},
unterliegt
q ∈ Q
Die Leistungsskalierungsfunktion kann verwendet werden, um jeden Punkt (machbar oder nicht machbar) auf der effizienten Grenze zu projizieren. Jeder Punkt (unterstützt oder nicht) kann erreicht werden. Der zweite Term in der Zielfunktion ist erforderlich, um ineffiziente Lösungen zu vermeiden. Fig. 3 zeigt, wie ein praktikabler Punkt g1 und ein unbrauchbarer Punkt g2 auf die nicht miteinander verbundenen Punkte q1 und q2 entlang der Richtung w projiziert werden, wobei eine Leistungs-Skalarisierungsfunktion verwendet wird. Die gestrichelten und die durchgezogenen Konturen entsprechen den Zielfunktionskonturen mit und ohne den zweiten Term der Zielfunktion.

Lösen von MCDM-Problemen
Verschiedene Denkschulen haben sich zur Lösung von MCDM-Problemen (sowohl des Design- als auch des Evaluierungstyps) entwickelt. Für eine bibliometrische Studie, die ihre Entwicklung im Laufe der Zeit zeigt, siehe Bragge, Korhonen, H. Wallenius und J. Wallenius [2010].

Mehrere objektive mathematische Programmierschule

(1) Vektormaximierung: Der Zweck der Vektormaximierung ist es, die nicht-dominierte Menge zu approximieren; ursprünglich entwickelt für Probleme der Mehrfachen Linearen Programmierung (Evans und Steuer, 1973; Yu und Zeleny, 1975).

(2) Interaktive Programmierung: Phasen der Berechnung alternieren mit Phasen der Entscheidungsfindung (Benayoun et al., 1971; Geoffrion, Dyer und Feinberg, 1972; Zionts und Wallenius, 1976; Korhonen und Wallenius, 1988). Es wird keine explizite Kenntnis der Wertfunktion des DM angenommen.

Goal Programmierschule

Ziel ist es, Zielvorgaben für Ziele festzulegen und gewichtete Abweichungen von diesen Zielen zu minimieren. Sowohl Bedeutungsgewichte als auch lexikographische Präventivgewichte wurden verwendet (Charnes und Cooper, 1961).

Fuzzy-Set-Theoretiker

Fuzzy-Sets wurden von Zadeh (1965) als eine Erweiterung der klassischen Vorstellung von Mengen eingeführt. Diese Idee wird in vielen MCDM-Algorithmen verwendet, um unscharfe Probleme zu modellieren und zu lösen.

Multi-Attribut-Dienstprogrammtheoretiker

Multi-Attribut-Dienstprogramm- oder -Wertfunktionen werden ausgelöst und verwendet, um die am meisten bevorzugte Alternative zu identifizieren oder um die Alternativen in einer Rangfolge zu ordnen. Aufwendige Interviewtechniken, die existieren, um lineare additive Nutzenfunktionen und multiplikative nichtlineare Nutzenfunktionen hervorzurufen, werden verwendet (Keeney und Raiffa, 1976).

Französische Schule

Die französische Schule konzentriert sich auf Entscheidungshilfen, insbesondere auf die ELECTRE-Familie der Outranking-Methoden, die Mitte der 1960er Jahre in Frankreich entstanden. Die Methode wurde zuerst von Bernard Roy (Roy, 1968) vorgeschlagen.

Evolutionäre multi-objektive Optimierungsschule (EMO)

EMO-Algorithmen beginnen mit einer Anfangspopulation und aktualisieren sie, indem sie Prozesse verwenden, die darauf abzielen, das natürliche Überleben der Fittest-Prinzipien und genetische Variationsoperatoren zu imitieren, um die durchschnittliche Population von einer Generation zur nächsten zu verbessern. Ziel ist es, eine Population von Lösungen zu erreichen, die die nicht-dominierte Menge repräsentieren (Schaffer, 1984; Srinivas und Deb, 1994). In jüngerer Zeit gibt es Bemühungen, Präferenzinformationen in den Lösungsprozess von EMO-Algorithmen zu integrieren (siehe Deb und Köksalan, 2010).

Analytischer Hierarchieprozess (AHP)

Die AHP zerlegt zuerst das Entscheidungsproblem in eine Hierarchie von Teilproblemen. Dann bewertet der Entscheider die relative Wichtigkeit seiner verschiedenen Elemente durch paarweise Vergleiche. Der AHP wandelt diese Bewertungen in numerische Werte (Gewichte oder Prioritäten) um, die verwendet werden, um eine Bewertung für jede Alternative zu berechnen (Saaty, 1980). Ein Konsistenz-Index misst das Ausmaß, in dem die Entscheidungsträger in ihren Antworten konsistent waren. AHP ist eine der umstrittensten Techniken, die hier aufgelistet sind, wobei einige Forscher in der MCDA-Gemeinschaft glauben, dass sie fehlerhaft ist. Die zugrundeliegende Mathematik ist auch komplizierter, obwohl sie als Ergebnis von kommerziell verfügbarer Software eine gewisse Popularität erlangt hat.

In mehreren Arbeiten wurde die Anwendung von MCDM-Techniken in verschiedenen Disziplinen wie Fuzzy-MCDM, klassisches MCDM, nachhaltige und erneuerbare Energie, VIKOR-Technik, Transportsysteme, Servicequalität, TOPSIS-Methode, Energiemanagementprobleme, E-Learning, Tourismus und Gastgewerbe, SWARA und WASPAS-Methoden.

MCDM-Methoden
Folgende MCDM-Methoden stehen zur Verfügung, von denen viele durch spezialisierte Entscheidungssoftware implementiert werden:

Aggregierte Index-Randomisierungsmethode (AIRM)
Analytischer Hierarchieprozess (AHP)
Analytischer Netzwerkprozess (ANP)
Beste schlechte Methode (BWM)
Merkmalsobjekte METhod (COMET)
Auswahl nach Vorteilen (CBA)
Datenumschlagsanalyse
Entscheidung EXpert (DEX)
Disaggregation – Aggregationsansätze (UTA *, UTAII, UTADIS)
Grobeinstellung (Grobeinstellung)
Dominanz-basierter Rough-Set-Ansatz (DRSA)
ELECTRE (Outranking)
Bewertung basierend auf der Entfernung von der Durchschnittslösung (EDAS)
Evidenzbasierter Ansatz (ER)
Zielprogrammierung (GP)
Graue relationale Analyse (GRA)
Inneres Produkt von Vektoren (IPV)
Attraktivität durch eine kategoriale Basiertevaluationstechnik (MACBETH) messen
Einfache Multi-Attribut-Bewertungsmethode (SMART)
Multi-Attribute Globale Ableitung von Qualität (MAGIQ)
Multi-Attribut-Dienstprogramm Theorie (MAUT)
Multi-Attribut-Wert-Theorie (MAVT)
Neue Methode zur Beurteilung (NATA)
Nichtstrukturelles Fuzzy Decision Support System (NSFDSS)
Potenziell alle paarweisen Rangierungen aller möglichen Alternativen (PAPRIKA)
PROMETHEE (Outranking)
Stochastische multikriterielle Akzeptanzanalyse (SMAA)
Superioritäts- und Minderwertigkeits-Ranking-Methode (SIR-Methode)
Technik für die Reihenfolge der Priorisierung durch Ähnlichkeit zur idealen Lösung (TOPSIS)
Wertanalyse (VA)
Werttechnik (VE)
VIKOR-Methode
Fuzzy-VIKOR-Methode
Gewichtetes Produktmodell (WPM)
Gewichtetes Summenmodell (WSM)
Rembrandt-Methode